How to Calculate RMSD for Protein Structure Comparison: A Guide for Structural Biologists and Drug Developers

Abstract

This article provides a comprehensive guide to calculating and interpreting the Root Mean Square Deviation (RMSD) for protein structure comparison, a fundamental task in structural biology, drug discovery, and protein modeling. It covers the foundational principles and mathematical formula of RMSD, detailed methodologies for practical calculation using common tools and algorithms, strategies for troubleshooting common pitfalls and optimizing alignments, and a comparative analysis of RMSD against other similarity metrics like TM-score and GDT. Aimed at researchers, scientists, and drug development professionals, this guide synthesizes current best practices to enable accurate quantification of structural similarities and differences.

What is RMSD? Understanding the Core Concepts of Protein Structural Similarity

Root Mean Square Deviation (RMSD) is a fundamental metric in structural biology and computational chemistry for quantifying the average distance between the atoms of two superimposed molecular structures. It provides a single, quantitative measure of structural similarity, serving as an essential tool for comparing three-dimensional protein conformations. The RMSD value, typically expressed in Angstroms (Ã…), is defined as the square root of the average squared distance between corresponding atoms in two optimally aligned structures. A value of 0 indicates identical structures, while increasing values reflect greater structural divergence [1] [2].

The significance of RMSD extends across multiple scientific domains, from assessing protein flexibility and conformational changes to evaluating the performance of computational modeling methods. In drug discovery, RMSD calculations help researchers understand ligand-binding interactions, analyze molecular dynamics trajectories, and validate structural predictions against experimental data. Its mathematical simplicity and intuitive interpretation have established RMSD as the gold standard for structural comparison, despite the development of complementary metrics [3] [4].

Mathematical Foundation and Calculation

The mathematical formulation of RMSD centers on the calculation of the root mean square of the minimal distances between corresponding atoms in two aligned structures. For two sets of atomic coordinates representing different conformations of the same molecule, the RMSD is calculated after optimal superposition to minimize the overall deviation [1].

Core Mathematical Formula

The standard RMSD formula for comparing two superimposed structures with n equivalent atoms is:

RMSD = √[ (1/n) × Σ(d_i)² ]

Where:

• n = number of atom pairs compared
• d_i = distance between the i-th pair of corresponding atoms
• Σ = summation over all n atom pairs [1] [3]

This calculation requires prior optimal superposition of the two structures, typically achieved through rotational and translational adjustments that minimize the RMSD value itself, a process known as the Kabsch algorithm [5].

Key Properties and Characteristics

RMSD possesses several mathematical properties that influence its application and interpretation:

• Non-negativity: RMSD values are always zero or positive, with zero representing perfect congruence [1]
• Sensitivity to outliers: Due to the squaring of distances, larger deviations contribute disproportionately to the final value [1] [3]
• Scale dependence: RMSD values are directly expressed in distance units (typically Ã…), making them dependent on the scale of the structures being compared [1]
• Dimensionality dependence: For proteins of different sizes, RMSD values are affected by the number of atoms included in the calculation [5]

Applications in Structural Biology and Drug Discovery

RMSD analysis provides critical insights across numerous research domains, serving as a versatile tool for structural comparison and validation.

Protein Structure Analysis

In structural bioinformatics, RMSD quantifies conformational differences between protein structures. This includes measuring structural divergence in homologous proteins, assessing conformational changes upon ligand binding, and evaluating protein flexibility through molecular dynamics simulations. The root mean square deviation of atomic positions represents the standard measure of the average distance between atoms of superimposed proteins [1] [5].

Drug Discovery and Development

RMSD plays several crucial roles in structure-based drug design:

• Docking validation: Comparing predicted ligand binding poses to experimental crystallographic data [1] [2]
• Molecular dynamics: Tracking conformational stability and changes during simulations of drug-receptor interactions [4]
• Virtual screening: Assessing structural similarity between candidate compounds and known active molecules [2]

Modeling Assessment

Community-wide initiatives such as CASP (Critical Assessment of protein Structure Prediction) and GPCR Dock employ RMSD as a primary metric for evaluating the accuracy of computational models against experimental reference structures [3].

Table 1: RMSD Interpretation Guidelines in Protein Studies

RMSD Range (Ã…)	Structural Relationship	Typical Applications
0 - 1.0	Very high similarity	Alternative conformations of the same protein; different experimental conditions
1.0 - 2.0	High similarity	Close homologs; different crystallization conditions
2.0 - 3.5	Moderate similarity	Distant homologs; conformational changes
> 3.5	Low similarity	Different folds; major conformational transitions

Normalization and Advanced RMSD Metrics

A significant limitation of standard RMSD is its dependence on protein size, making comparisons across different-sized structures problematic. A normalized RMSD metric was developed to address this issue, enabling more meaningful comparisons between proteins of varying lengths [5].

Normalization Approaches

Several normalization strategies have been developed to enhance the comparability of RMSD values:

• Length-dependent normalization: Adjusts RMSD values to equivalent statistical significance for different protein lengths, such as the RMSD100 approach which normalizes to the value expected for a 100-residue protein [5] [6]
• Range normalization: Divides RMSD by the range of the observed data (NRMSD) [1]
• Mean normalization: Expressed as a percentage of the mean observed value (CV(RMSD)) [1]
• Interquartile range normalization: Divides RMSD by the interquartile range to reduce sensitivity to extreme values [1]

Table 2: Normalized RMSD Variants and Applications

Metric	Formula	Application Context
NRMSD	RMSD / (yₘₐₓ - yₘᵢₙ)	Comparison across different scales
CV(RMSD)	RMSD / ȳ	Percentage-based comparison
RMSD100	Normalized to 100 residues	Comparing proteins of different lengths
RMSDIQR	RMSD / IQR	Reduced sensitivity to outliers

Experimental Protocols and Methodologies

Standard Protocol for RMSD Calculation Between Two Protein Structures

Objective: Calculate the backbone RMSD between two conformations of the same protein to quantify structural differences.

Materials and Software Requirements:

Table 3: Essential Research Reagents and Computational Tools

Resource	Type	Function
PyMOL	Visualization software	Structure visualization and analysis
MAMMOTH	Structural alignment algorithm	Optimal structure superposition
GROMACS	Molecular dynamics package	Trajectory analysis and RMSD calculation
RCSB PDB	Structural database	Source of experimental reference structures
ChimeraX	Molecular visualization	Interactive structure comparison

Step-by-Step Procedure:

• Structure Preparation

  • Obtain atomic coordinates for both structures in PDB format
  • Remove heteroatoms (water, ions, ligands) unless specifically relevant to analysis
  • Ensure identical atom selection and numbering between structures

• Atom Selection

  • Select equivalent atoms for comparison (typically Cα atoms for backbone RMSD)
  • Verify sequence correspondence between structures
  • Note the number of atom pairs (n) included in the calculation

• Optimal Superposition

  • Apply the Kabsch algorithm for rotational and translational alignment
  • Minimize the sum of squared distances between corresponding atoms
  • Iteratively refine alignment if using outlier-resistant methods

• Distance Calculation and RMSD Computation

  • Calculate Euclidean distances between all corresponding atom pairs
  • Square each distance value
  • Compute the mean of squared distances
  • Take the square root to obtain the final RMSD value

• Validation and Interpretation

  • Visually inspect the quality of structural alignment
  • Compare RMSD value to appropriate benchmarks for the system
  • Consider complementary metrics (GDT, MaxSub) for full assessment

Troubleshooting Notes:

• High RMSD values may indicate poor alignment rather than true structural differences
• Mismatched atom selections will produce artificially elevated RMSD
• Flexible regions disproportionately influence global RMSD; consider core-only analysis

Protocol for Time-Resolved RMSD Analysis in Molecular Dynamics

Objective: Monitor conformational stability and changes throughout MD simulations.

Procedure:

• Trajectory Preparation: Align all simulation frames to a reference structure (usually the initial frame or average structure) to remove global translation and rotation
• Reference Selection: Choose an appropriate reference structure for comparison (typically the starting structure or a representative conformation)
• Frame-by-Frame Calculation: Compute RMSD between each trajectory frame and the reference structure
• Time Series Analysis: Plot RMSD as a function of simulation time to identify equilibration, stability, and conformational transitions
• Statistical Analysis: Calculate average RMSD, fluctuations, and distribution characteristics for stable simulation segments

Limitations and Complementary Metrics

While RMSD remains the most widely used structural comparison metric, several limitations necessitate complementary approaches:

Key Limitations

• Sensitivity to outliers: A small number of highly deviating regions can dominate the RMSD value, obscuring overall similarity [3]
• Size dependence: Larger proteins tend to have higher RMSD values, complicating cross-protein comparisons [5]
• Global measure: RMSD may poorly represent local similarities, especially in flexible proteins with domain movements [3]
• Alignment dependence: Results are highly sensitive to the quality and method of structural alignment [3] [6]

Alternative and Complementary Metrics

• Global Distance Test (GDT): Measures the largest set of residues that superimpose under defined distance cutoffs, more focused on common core than outliers [6]
• MaxSub: Identifies the largest well-overlapped subset of the protein [6]
• Template Modeling Score (TM-score): Size-independent metric that emphasizes spatial proximity of closer residues [7]
• Local Distance Difference Test (lDDT): Residue-based evaluation without requiring superposition [3]

Root Mean Square Deviation remains an indispensable tool for quantifying structural relationships in macromolecular research. Its mathematical clarity, computational efficiency, and intuitive interpretation have secured its position as the gold standard for structural comparison across diverse applications from basic structural biology to drug discovery. While aware of its limitations, researchers continue to rely on RMSD as a primary metric, enhanced by normalization approaches and complementary measures when appropriate. As structural biology advances with cryo-EM and AI-based structure prediction, RMSD maintains its fundamental role in validating and comparing three-dimensional molecular architectures.

Root Mean Square Deviation (RMSD) is a foundational metric in computational structural biology, providing a quantitative measure of the average distance between atoms in superimposed protein structures. For researchers and drug development professionals, RMSD serves as a crucial tool for assessing structural similarity, evaluating protein structure predictions, analyzing molecular dynamics simulations, and understanding ligand-induced conformational changes. The RMSD value, expressed in Angstroms (Ã…), offers a single numerical representation of structural differences, where a value of 0 indicates perfect superposition and increasing values reflect greater structural divergence [1] [3]. In the context of protein structure comparison research, accurately calculating and interpreting RMSD is essential for validating computational models, assessing docking predictions, and understanding structure-function relationships that underpin drug discovery efforts.

The importance of RMSD extends across multiple domains within structural biology. In protein structure prediction assessments like CASP (Critical Assessment of Structure Prediction), RMSD provides an objective standard for evaluating model accuracy against experimental reference structures [3]. In structure-based drug design, RMSD calculations help quantify how closely a docked ligand conformation matches experimental observations, guiding lead optimization efforts [1] [8]. Furthermore, in molecular dynamics simulations, RMSD analysis tracks conformational changes over time, revealing insights into protein flexibility, folding pathways, and functional mechanisms [2]. Despite the development of alternative metrics such as TM-score and GDT, RMSD remains widely used due to its mathematical simplicity, intuitive interpretation, and historical establishment within the structural biology community [9] [10].

Mathematical Foundation of RMSD

Core RMSD Formula

The Root Mean Square Deviation represents the square root of the arithmetic mean of the squares of the deviations between corresponding atomic positions. For two superimposed sets of atomic coordinates, the RMSD is mathematically defined as:

RMSD = √[ (1/n) × Σᵢ(Δxᵢ² + Δyᵢ² + Δzᵢ²) ]

Where:

• n represents the total number of atom pairs included in the calculation
• Σᵢ denotes the summation over all n atom pairs
• Δxáµ¢, Δyáµ¢, Δzáµ¢ represent the differences in x, y, and z coordinates between the i-th pair of corresponding atoms after optimal superposition [1] [11]

This formula can be equivalently expressed in terms of the Euclidean distances between corresponding atom pairs:

RMSD = √[ (1/n) × Σᵢ(dᵢ²) ]

Where dáµ¢ represents the Euclidean distance between the i-th pair of corresponding atoms after superposition [3]. This formulation highlights that RMSD essentially measures the root mean square of the straight-line distances between equivalent atoms in the two structures being compared.

Calculation Methodology

The computation of RMSD between two protein structures involves a systematic multi-step process that ensures accurate and meaningful comparison:

• Atom Selection and Correspondence: The first critical step involves identifying which atoms to include in the calculation and establishing one-to-one correspondence between equivalent atoms in the two structures. For protein backbone comparisons, this typically involves Cα atoms, while all-atom RMSD includes all non-hydrogen atoms [3] [10].

• Structural Superposition: The two structures are optimally aligned through translation and rotation to minimize the RMSD value itself. This is typically achieved using algorithms like the Kabsch method, which finds the optimal rotation matrix that minimizes the sum of squared distances between corresponding atoms [2].

• Distance Calculation: After superposition, the Euclidean distances between each pair of corresponding atoms are calculated using the standard distance formula in three-dimensional space.

• Averaging and Root Extraction: The squared distances are summed, averaged by dividing by the number of atom pairs, and the square root of this average provides the final RMSD value [1] [11].

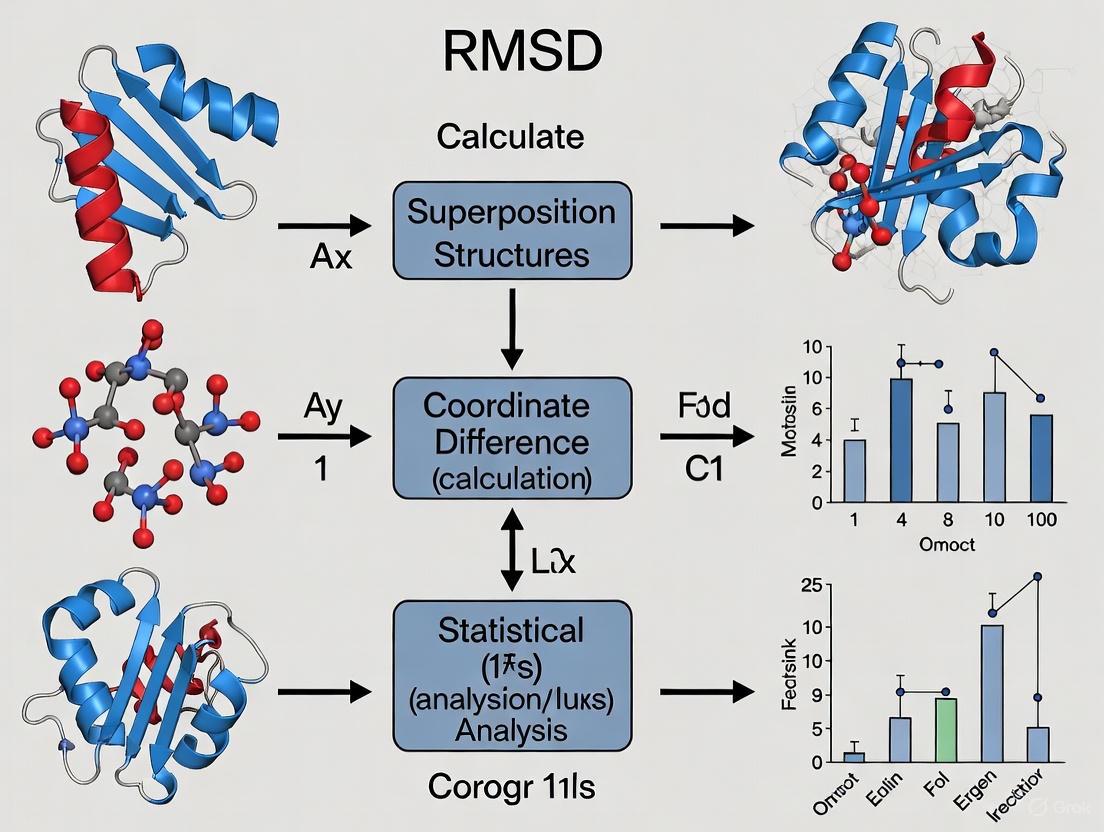
The following workflow illustrates the complete RMSD calculation process:

Research Applications in Protein Science

Protein Structure Comparison and Model Validation

RMSD serves as a fundamental metric for comparing experimental protein structures and validating computational models. In the protein structure prediction assessment (CASP), RMSD provides an objective measure to evaluate the accuracy of predicted models against experimentally determined reference structures [3]. Similarly, when comparing different experimental structures of the same protein determined under varying conditions (e.g., with different ligands, pH, or crystal forms), RMSD quantifies conformational changes and flexibility. The distribution of backbone RMSD values for experimentally determined structure pairs of identical proteins typically ranges from 0 to 1.2 Å, reflecting inherent protein flexibility and experimental resolution limits [3]. For homology modeling, RMSD values below 2.0 Å for Cα atoms generally indicate high-quality models, particularly when closely related structural templates are available [9].

Molecular Dynamics and Conformational Analysis

In molecular dynamics (MD) simulations, RMSD analysis tracks structural evolution and stability over time. By calculating RMSD between simulation frames and a reference structure (typically the initial minimized structure), researchers monitor conformational sampling, convergence, and structural deviations. This application reveals protein folding pathways, functional motions, and ligand-induced conformational changes [2]. Time-resolved RMSD analysis can identify stable conformational states, transition points, and equilibrium behavior, providing insights into the relationship between protein dynamics and biological function. The sensitivity of RMSD to larger structural changes makes it particularly valuable for detecting major conformational transitions in simulated systems.

Drug Discovery and Docking Assessment

In structure-based drug design, RMSD calculations play a crucial role in evaluating docking predictions and virtual screening results. For protein-ligand docking, heavy-atom RMSD between predicted and experimental ligand conformations assesses docking accuracy and scoring function performance [1] [8]. Lower ligand RMSD values indicate more reliable pose predictions, with values below 2.0 Ã… generally considered successful in virtual screening applications. Additionally, RMSD analysis of protein binding sites helps quantify backbone and sidechain rearrangements upon ligand binding, revealing induced-fit mechanisms and allosteric effects that influence drug binding and specificity [8].

Table 1: RMSD Interpretation Guidelines in Protein Structure Comparison

RMSD Range	Structural Interpretation	Typical Applications
< 1.0 Ã…	Very high similarity; minimal structural differences	Same protein under different conditions; high-quality model validation
1.0 - 2.0 Ã…	High similarity; minor conformational variations	Close homologs; accurate homology models; ligand-induced changes
2.0 - 3.0 Ã…	Moderate similarity; significant local differences	Distant homologs; medium-quality models; domain movements
> 3.0 Ã…	Low similarity; major structural differences	Different folds; poor models; substantial conformational changes

Experimental Protocol for RMSD Calculation

Structure Preparation and Preprocessing

Proper structure preparation is essential for meaningful RMSD calculations. Begin by selecting appropriate protein structures from the Protein Data Bank (PDB) or computational models. Remove heteroatoms including water molecules, ions, and small molecules unless specifically relevant to the analysis. Ensure both structures contain identical atom sets with consistent atom naming and numbering conventions. For protein backbone RMSD, select Cα atoms exclusively; for all-atom RMSD, include all non-hydrogen atoms. Identify and handle missing residues or atoms appropriately, either by excluding incomplete regions or using modeling tools to reconstruct missing coordinates. Verify that both structures have the same number of atoms selected for comparison to ensure valid one-to-one correspondence [2] [10].

Structural Alignment Procedures

Structural alignment optimizes the superposition of two structures to minimize the RMSD value. Implement the Kabsch algorithm for optimal rigid-body alignment, which involves:

• Translation: Center both structures at the origin by subtracting their centroids from all atomic coordinates.
• Covariance Matrix Calculation: Compute the covariance matrix H between the two centered coordinate sets.
• Rotation Matrix Determination: Perform singular value decomposition (SVD) of H to obtain the optimal rotation matrix.
• Coordinate Transformation: Apply the rotation matrix to the second structure to align it with the first structure.

For complex structural comparisons involving domain movements or flexible regions, consider iterative superposition methods that assign lower weights to highly deviating regions. Alternatively, use flexible alignment algorithms like FATCAT that introduce twists between rigid domains to better align structures with internal flexibility [10]. Visually inspect the aligned structures to verify the biological reasonableness of the superposition before proceeding with RMSD calculation.

RMSD Computation and Validation

After optimal superposition, calculate the RMSD using the standard formula. Compute both global RMSD (all selected atoms) and regional RMSD values for specific structural elements (e.g., binding sites, secondary structure elements) to gain comprehensive insights. Validate RMSD calculations by comparing results from multiple software packages (PyMOL, ChimeraX, VMD) to ensure consistency. Perform sensitivity analysis by testing how RMSD values change with different atom selections or alignment methods. Cross-reference RMSD values with other similarity metrics like TM-score or GDT for a more comprehensive assessment of structural similarity [9] [10].

Table 2: Research Reagent Solutions for RMSD Analysis

Tool/Category	Specific Examples	Function in RMSD Analysis
Structural Biology Software	PyMOL, ChimeraX, VMD	Visualization, structural alignment, and RMSD calculation
Web-Based Platforms	RCSB PDB Pairwise Alignment, CSAlign	Accessible RMSD calculation without local software installation
Programming Libraries	BioPython, MDAnalysis	Automated, high-throughput RMSD analysis in scripts
Specialized Algorithms	Kabsch, FATCAT, CE	Optimal structural superposition for RMSD minimization
Structure Datasets	PDB, AlphaFold Database	Source of experimental and predicted structures for comparison

Interpretation and Limitations

Contextual Interpretation of RMSD Values

Interpreting RMSD values requires careful consideration of biological context, comparison scale, and research objectives. For global protein structure comparisons, RMSD values below 2.0 Å typically indicate highly similar structures, while values exceeding 3.0 Å suggest significant structural differences [9]. However, these thresholds vary depending on protein size, comparison scope, and scientific question. Regional RMSD analysis often provides more biologically relevant insights than global RMSD alone, particularly when comparing specific functional domains or binding sites. Additionally, consider inherent protein flexibility—regions with high conformational variability (e.g., surface loops) naturally exhibit higher RMSD values without necessarily indicating poor model quality or biological insignificance [3].

The relationship between RMSD and structural similarity is not linear, and RMSD values should be interpreted relative to protein size. For large proteins or complexes, slightly higher RMSD values may still represent biologically relevant similarities, while for small proteins or ligands, even sub-Angstrom differences might be significant. Always correlate RMSD findings with visual inspection of aligned structures and complementary metrics like TM-score, which normalizes for protein size and provides a more intuitive similarity score between 0 and 1 [9] [10].

Limitations and Complementary Metrics

Despite its widespread use, RMSD has several limitations that researchers must acknowledge. RMSD is highly sensitive to outliers—a small number of highly deviating regions can disproportionately increase the global RMSD, masking overall structural similarity [1] [3]. This outlier sensitivity makes RMSD less suitable for comparing structures with localized flexibility or conformational changes. Additionally, RMSD is scale-dependent, making comparisons across different proteins or datasets problematic. RMSD also decreases with increasing number of atoms included in calculations, potentially leading to misleading comparisons between analyses with different atom selections [12].

To address these limitations, complement RMSD with alternative metrics:

• TM-score: Provides length-independent structural similarity assessment, with values above 0.5 indicating same fold and below 0.17 indicating random similarity [9] [10].
• GDT (Global Distance Test): Measures the percentage of residues within specified distance cutoffs, offering a more robust assessment of global fold similarity [9].
• LDDT (Local Distance Difference Test): Evaluates local structural quality by comparing distance maps, remaining reliable even with domain movements [9].

The following decision tree guides the selection of appropriate structural similarity metrics:

Advanced Considerations and Future Directions

Normalization Strategies for Enhanced Comparability

Normalizing RMSD values facilitates more meaningful comparisons across different protein systems and scales. Common normalization approaches include dividing RMSD by the range of the measured data (maximum minus minimum values) or by the mean of the observed values [1]. The Normalized RMSD (NRMSD) is calculated as:

NRMSD = RMSD / (yₘₐₓ - yₘᵢₙ)

Alternatively, researchers may calculate the Coefficient of Variation of RMSD:

CV(RMSD) = RMSD / ȳ

Where ȳ represents the mean of the observed values [1]. For structural comparisons, normalization by protein length or diameter provides more comparable metrics across different sized proteins. Another robust approach divides RMSD by the interquartile range (IQR) to reduce sensitivity to extreme values:

RMSD/IQR = RMSD / (Q₃ - Q₁)

Where Q₁ and Q₃ represent the first and third quartiles of distance distributions [1]. These normalization strategies enhance the comparability of RMSD values across different studies, protein systems, and experimental conditions.

Emerging Methodologies and Future Developments

The field of structural comparison continues to evolve with emerging methodologies enhancing RMSD analysis and application. Machine learning approaches increasingly incorporate RMSD-derived features for protein structure prediction and quality assessment [2]. Artificial intelligence-powered alignment algorithms can identify optimal superpositions more efficiently than traditional methods, while ensemble-based RMSD calculations account for structural dynamics by comparing multiple conformational states simultaneously [2].

Advances in structural biology techniques, particularly cryo-electron microscopy (cryo-EM), present new opportunities and challenges for RMSD applications. As cryo-EM structures often exhibit regional resolution variations, development of resolution-weighted RMSD calculations represents an active research direction [2]. Similarly, integrative structural biology approaches that combine data from multiple experimental sources (X-ray crystallography, NMR, cryo-EM, cross-linking mass spectrometry) require specialized RMSD approaches that accommodate different uncertainty characteristics across structural regions [2]. Future RMSD methodologies will likely incorporate Bayesian frameworks to explicitly account for positional uncertainties, providing more statistically rigorous structural comparisons that reflect the inherent limitations of both experimental and computational structural models.

Root-Mean-Square Deviation (RMSD) is a fundamental metric in structural biology that quantifies the average distance between atoms of two superimposed three-dimensional structures. For proteins, this typically involves calculating the displacement between equivalent Cα atoms after optimal rigid-body superposition. The mathematical formulation for RMSD is expressed as RMSD = √[Σ(di)²/N], where di represents the distance between the i-th pair of equivalent atoms and N is the total number of atom pairs compared [3] [13]. Despite its apparent simplicity, the problem of quantifying differences between protein structures is non-trivial and continues to evolve with new methodologies [3]. RMSD provides a single summary value measured in Ångströms (Å), where 0 indicates identical structures and increasing values reflect greater structural dissimilarity [13] [9].

The significance of RMSD extends beyond mere geometric comparison. As articulated by, two protein conformations can be considered intrinsically similar only if their RMSD is smaller than that obtained when one structure is mirror-inverted [14]. This conceptual framework establishes RMSD as a meaningful indicator of overall chain folding patterns and structural conservation. While RMSD remains the most popular measure for structural comparison, it is dominated by the largest errors present in compared structures, which has led to the development of complementary metrics and methods to address its limitations [3].

Key Applications of RMSD

Assessment of Computational Models in Structure Prediction

RMSD serves as a primary validation metric in community-wide blind assessments of protein structure prediction methods such as CASP (Critical Assessment of protein Structure Prediction) and GPCR Dock [3]. In these evaluations, computational models are compared to experimentally determined reference structures using RMSD among other measures. The distribution of backbone RMSD values for accurate models typically ranges around 2.3 Ã… for homology modeling cases with close sequence relatives (~40% identity), with values increasing for more distantly related templates [3]. The Global Distance Test (GDT), a derivative metric, calculates the percentage of residues within certain distance cutoffs (typically from 0.5 Ã… to 10.0 Ã…) after superposition, providing a more robust assessment of model quality than RMSD alone, particularly for proteins with conformational flexibility [9].

Table 1: RMSD Interpretation Guidelines for Model Assessment

RMSD Value	Interpretation	Model Quality Assessment
<2 Ã…	High atomic-level accuracy	Very similar or identical structures; successful prediction
2-4 Ã…	Moderate residue-level accuracy	Structurally similar but not identical; quality depends on required resolution
>4 Ã…	Low domain-level accuracy	Structurally different; generally unacceptable for most applications

Analysis of Protein Flexibility and Conformational Changes

RMSD analysis reveals fundamental insights into protein dynamics and flexibility by quantifying conformational differences between structures of identical proteins determined under varying conditions. Experimental evidence from the Protein Data Bank shows that the majority of identical protein pairs exhibit RMSD values ranging from 0 to 1.2 Å due to inherent protein flexibility and experimental resolution limits [3]. Significantly higher RMSD values indicate substantial conformational rearrangements, such as those occurring between active and inactive states of receptors. For example, the active and inactive conformations of estrogen receptor α exhibit large global backbone RMSD values despite differing primarily in the position of a single helix, demonstrating how RMSD can capture functionally relevant structural transitions [3].

Evaluation of Protein-Ligand Docking Results

In molecular docking assessments, RMSD provides a crucial measure of docking accuracy by quantifying the spatial proximity between predicted and experimentally determined ligand binding poses. The CAPRI (Critical Assessment of PRedicted Interactions) community experiment employs RMSD among other metrics to evaluate docking predictions [3]. For protein-drug complexes in molecular dynamics simulations, RMSD analysis tracks the stability of protein structures across different ligand interactions, revealing how identical proteins can exhibit varying RMSD profiles when complexed with different drugs due to simulation randomness and specific interaction patterns [15]. This application is particularly valuable in drug discovery for comparing how a common protein target responds to different therapeutic compounds.

Evolutionary Studies and Structural Genomics

While sequence similarity traditionally guides evolutionary studies, RMSD-based structural comparisons often reveal conserved folds and functional relationships even when sequence identity falls below 25% [9]. This capability is particularly valuable for identifying distant evolutionary relationships that are undetectable through sequence analysis alone. Structural comparison tools like FoldSeek and SARST2 leverage RMSD-like metrics to identify proteins with similar folds despite minimal sequence similarity, enabling more comprehensive evolutionary analyses [16] [9]. The TM-score, which normalizes RMSD by protein length, provides a more reliable measure for detecting common folds across evolutionarily related proteins, with scores above 0.5 indicating generally the same fold [9].

Experimental Protocols for RMSD Calculation

Theoretical Foundation and Algorithm Selection

The standard protocol for RMSD calculation involves three critical steps: structural alignment, optimal superposition, and distance calculation. The Kabsch algorithm provides the mathematical foundation for determining the optimal rotation matrix that minimizes the RMSD between two sets of coordinate points [13]. This algorithm operates through a sequence of steps: (1) translation of both structures to place their geometric centers at the origin (x=0, y=0, z=0), (2) computation of the covariance matrix between the two coordinate sets, and (3) derivation of the optimal rotation matrix through singular value decomposition [13]. The quaternion algorithm represents an alternative approach for solving the same superposition problem [13].

Table 2: Research Reagent Solutions for Structural Analysis

Research Reagent	Function in RMSD Analysis
PDB Structure Files	Source of atomic coordinates for reference and model structures (e.g., 1Y3N, 1Y3Q)
Cα Atom Selection	Standard reference points for backbone structure comparison
Kabsch Algorithm	Computational method for optimal rigid-body superposition
Molecular Visualization Software	Visual assessment of structural alignment quality
Molecular Dynamics Trajectories	Time-dependent structural data for RMSD fluctuation analysis

Practical Implementation Using Python and NumPy

The following protocol provides a step-by-step methodology for calculating RMSD between two protein structures:

• Structure Preparation: Obtain PDB files for both reference and model structures. Select equivalent atoms for comparison (typically Cα atoms for backbone analysis).

• Coordinate Extraction: Parse PDB files to extract Cartesian coordinates for selected atoms using a PDB reader module.

• Centering Structures: Translate both structures to place their centroids at the coordinate origin:

• Calculate Covariance Matrix:

• Singular Value Decomposition:

• Ensure Proper Rotation (remove mirroring):

• Apply Rotation and Calculate RMSD:

This implementation produces both the RMSD value and the aligned coordinates for visualization [13].

Workflow for Comparative Analysis

The following diagram illustrates the complete RMSD calculation workflow:

Complementary Metrics and Methodological Considerations

Limitations of RMSD and Alternative Approaches

Despite its widespread use, RMSD has significant limitations that researchers must consider. RMSD is highly sensitive to outliers, meaning that a small number of deviating regions can disproportionately influence the overall value [3]. This is particularly problematic when comparing structures with flexible termini, loops, or relative domain movements. Additionally, RMSD values are length-dependent, making comparisons across different-sized proteins challenging. To address these limitations, several complementary metrics have been developed:

• TM-score: A length-normalized metric that provides a more balanced assessment of global fold similarity, with scores ranging from 0 to 1 (where >0.5 indicates the same fold) [9].
• GDT (Global Distance Test): Calculates the percentage of residues within specified distance cutoffs, offering a more robust measure for model quality assessment [9].
• LDDT (Local Distance Difference Test): Evaluates local structural quality by comparing distance distributions in a superposition-independent manner, making it particularly valuable for assessing structures with domain movements [9].

Integration with Contact-Based Measures

Contact-based measures offer a superposition-independent alternative to RMSD by quantifying the similarity of residue-residue contact patterns between structures [3]. These methods are often more robust against structural outliers and better capture the fundamental nature of protein folding determinants. Modern structural alignment tools like SARST2 integrate multiple approaches, combining primary sequence, secondary structure elements, and tertiary contact information to achieve both accuracy and efficiency in massive database searches [16]. The integration of RMSD with contact-based measures provides a more comprehensive framework for structural comparison in evolutionary studies and model assessment.

RMSD remains an indispensable tool in structural biology, providing a straightforward, interpretable measure of structural similarity with critical applications across protein modeling, docking, dynamics analysis, and evolutionary studies. While its limitations necessitate complementary approaches like TM-score and contact-based measures, RMSD continues to offer fundamental insights into protein structure and function. As structural databases expand with AI-predicted models, efficient RMSD calculation and interpretation will remain essential skills for researchers navigating the era of structural big data. The protocols and applications outlined herein provide a foundation for the rigorous application of RMSD in scientific research and drug development.

Root Mean Square Deviation (RMSD) is a fundamental metric in structural biology for quantifying the similarity between two protein structures. The utility and interpretation of an RMSD value are profoundly influenced by the selection of atoms used in the calculation. This application note provides a detailed protocol for researchers, focusing on the strategic selection of atoms—from the common Cα and backbone atoms to more specialized subsets—to ensure that RMSD measurements are both accurate and biologically meaningful. Proper atomic selection is critical for applications ranging from assessing protein folding and conformational changes to validating computational models against experimental structures.

Core Concepts of RMSD

The Root Mean Square Deviation (RMSD) provides a quantitative measure of the average distance between the atoms of two superimposed protein structures. The standard formula for calculating RMSD between two sets of coordinates, ( v ) and ( w ), for ( n ) equivalent atoms is:

[ \mathrm{RMSD} = \sqrt{\frac{1}{n}\sum{i=1}^{n}\|vi - wi\|^2} = \sqrt{\frac{1}{n}\sum{i=1}^{n}((v{ix}-w{ix})^2+(v{iy}-w{iy})^2+(v{iz}-w{iz})^2)} ]

The result is expressed in length units, typically Ångströms (Å), where 1 Å equals 10^(-10) m [17]. Before calculating RMSD, the two structures must be optimally superimposed via a rigid body transformation (translation and rotation) that minimizes this very RMSD value. Algorithms such as the Kabsch algorithm or quaternion-based methods are commonly used for this purpose [17].

Atomic Selection Strategies

The choice of which atoms to include in the RMSD calculation is a critical methodological decision that can define the metric's relevance to the biological question at hand. The table below summarizes the common atomic selections and their primary applications.

Table 1: Standard Atomic Selections for RMSD Calculation

Atomic Selection	Atoms Included	Primary Applications	Key Advantages	Considerations
Cα Atoms	Cα only	Global fold comparison, protein folding studies, model validation in CASP [17].	Simplified backbone representation; reduces noise from flexible side chains.	Insensitive to changes in side-chain orientations or backbone details.
Backbone Atoms	N, Cα, C, O	Refined backbone conformation analysis, loop modeling assessment.	More detailed description of the backbone geometry than Cα alone.	Can be skewed by mobile termini or flexible loops.
All Heavy Atoms	All non-hydrogen atoms	High-resolution comparison, ligand-binding site analysis, side-chain packing evaluation.	Most comprehensive structural assessment.	Highly sensitive to side-chain rotamer changes; can overstate differences.
Specific Subsets	User-defined (e.g., binding pocket residues, transmembrane helices)	Local structure validation, functional site analysis, domain movement studies [3].	Directly targets a relevant region; minimizes dilution of signal by irrelevant regions.	Requires careful definition of the subset; results are specific to that region.

Quantitative Comparison of Selection Impact

The choice of atomic selection directly influences the magnitude of the RMSD value and its statistical distribution. The following table synthesizes quantitative data from large-scale analyses to guide the interpretation of RMSD values.

Table 2: Interpretation of RMSD Values Based on Atomic Selection and Context

Context	Cα RMSD Range (Å)	Interpretation	Reference/Context
Experimental Noise & Native Flexibility	0 - 1.2 Ã…	Very similar structures; differences likely due to inherent flexibility or experimental resolution limits [3].	Distribution for pairs of identical experimental PDB structures.
High-Quality Homology Models	~2.3 Ã…	Representative of good model accuracy when a close homolog template is available (>40% sequence identity) [3].	Comparison of best GPCR Dock 2010 models to experimental answers.
Structurally Similar Pairs	1.0 - 3.0 Ã…	Moderate structural differences, potentially indicating biologically relevant conformational changes [2].	General guidance for comparative analysis.
Substantial Structural Differences	>3.0 Ã…	Large conformational changes or potentially different folds [2].	General guidance for comparative analysis.

Detailed Experimental Protocols

Protocol 1: Calculating Global RMSD for Model Validation

This protocol is designed for a standard assessment of a computational model against a reference experimental structure, commonly used in initiatives like CASP.

• Structure Preparation:

  • Obtain the PDB files for the reference structure and the model.
  • Using a tool like MOPAC or a Python script, ensure both structures contain the same protein chain and residues. Remove non-protein atoms (water, ions, ligands) unless they are the specific focus of the study [18] [2].
  • Verify that the sequence of residues is identical and the atom naming conventions are consistent between the two files.

• Atomic Selection:

  • For a global Cα RMSD, extract the coordinates of all Cα atoms from both structures.
  • For a global backbone RMSD, extract the coordinates of the N, Cα, C, and O atoms for all residues.

• Structure Superimposition:

  • Apply an algorithm (e.g., Kabsch) to perform optimal rigid body superposition of the model onto the reference structure, using the selected atoms. The goal is to find the rotation and translation that minimizes the RMSD between the two sets of coordinates [17].

• RMSD Calculation:

  • Using the superimposed coordinates, calculate the RMSD via the standard formula.
  • The final RMSD value is a single number representing the average distance between the selected atoms in the two structures after optimal alignment.

Protocol 2: Calculating Local RMSD for Functional Analysis

This protocol is used to focus on a specific, functionally important region of the protein, such as an active site or a binding pocket.

• Region Definition:

  • Identify the residues that constitute the region of interest (e.g., catalytic triad, ligand-binding pocket, a specific loop).

• Structure Preparation and Trimming:

  • Prepare the structures as in Protocol 1.
  • Trim the structures to include only the defined subset of residues. Some tools automatically handle this when a residue list is provided [3].

• Local Superimposition and Calculation:

  • Option A (Recommended for local similarity): Superimpose the entire structures using the global method (Protocol 1), then calculate the RMSD only for the atoms in the local subset using the resulting coordinates.
  • Option B (For isolated local comparison): Superimpose the structures using only the atoms in the local subset, then calculate the RMSD for that same subset. This ensures the alignment is optimized for the local region, ignoring the rest of the structure.

• Interpretation:

  • Compare the local RMSD to the global RMSD. A significantly lower local RMSD indicates that the region of interest is more accurately modeled or more structurally conserved than the protein as a whole.

Decision Workflow for Atomic Selection

The following diagram outlines a logical workflow to guide researchers in selecting the most appropriate atoms for their RMSD calculation.

The Scientist's Toolkit: Research Reagents & Solutions

Table 3: Essential Tools for Protein Structure Comparison and RMSD Analysis

Tool / Resource	Type	Primary Function	Application Note
PyMOL / ChimeraX	Visualization & Analysis Software	GUI-based structure visualization, superposition, and RMSD calculation.	Ideal for interactive analysis, visual inspection of alignments, and calculating RMSD on user-selected subsets.
GraSR [19]	Alignment-free Graph Neural Network	Fast protein structure comparison via learned representations.	Useful for extremely large-scale comparisons where traditional alignment is too slow; provides an alternative similarity metric.
SARST2 [16]	Structural Alignment Search Algorithm	Accurate and rapid alignment against massive databases.	Employs a filter-and-refine strategy, integrating primary to tertiary features for efficient database searches on ordinary computers.
EnsembleFlex [20]	Ensemble Analysis Suite	Analyzes conformational heterogeneity from structural ensembles.	Performs backbone and side-chain flexibility analysis via RMSD and RMSF (Root Mean Square Fluctuation) across multiple structures.
BioPython	Python Library	Programmatic parsing of PDB files and basic RMSD calculation.	Provides flexibility for custom analysis pipelines and batch processing of multiple structures.
LGA (Local-Global Alignment) [3]	Superimposition Algorithm	Iterative method to find the largest superimposable core.	Attenuates the effect of outlier regions by focusing on locally similar segments, addressing a key drawback of global RMSD.
Lonitoclax	Lonitoclax, CAS:2952589-57-8, MF:C43H45ClN4O5, MW:733.3 g/mol	Chemical Reagent	Bench Chemicals
Ganoderic acid L	Ganoderic acid L, MF:C30H46O8, MW:534.7 g/mol	Chemical Reagent	Bench Chemicals

Advanced Considerations and Complementary Metrics

While RMSD is a ubiquitous measure, it has known limitations. It is dominated by the largest errors in the structure, meaning that a single deviating loop can result in a high global RMSD, obscuring the high accuracy of the remainder of the model [3]. This is illustrated by pairs of structures like the active and inactive conformations of estrogen receptor α, which have a high global RMSD due to the movement of a single helix, making them indistinguishable by this metric alone from pairs with many small, scattered errors [3].

To address these issues, researchers should consider:

• Iterative Superimposition Methods: Algorithms like LGA (Local-Global Alignment) assign lower weights to the most deviating fragments, iteratively finding the largest superimposable core. This provides a more robust measure of similarity for proteins with localized flexibility [3].
• Complementary Metrics:
  • TM-score: A superposition-based metric that is less sensitive to local errors and provides a more global measure of fold similarity.
  • GDT (Global Distance Test): Measures the average percentage of residues under a specified distance cutoff, favored in CASP for model assessment [17] [3].
  • Contact-Based Measures: These superimposition-independent methods quantify similarity based on residue-residue contact maps, making them robust against local structural variations [3].

The precise selection of atoms is not merely a technical prelude but the foundation of a biologically insightful RMSD analysis. A deliberate strategy—choosing Cα atoms for global fold assessment, backbone atoms for detailed backbone conformation, specific subsets for functional regions, and employing advanced methods to handle flexibility—ensures that the calculated RMSD accurately reflects the structural features of interest. By integrating these atomic selection protocols with an understanding of complementary metrics, researchers can leverage RMSD as a powerful, precise tool in structural biology and drug development.

The Critical Role of Optimal Superposition in RMSD Calculation

The Root Mean Square Deviation (RMSD) of atomic positions is the cornerstone metric for quantifying geometric differences between two protein structures. Its calculation, however, is not merely a direct measurement of distances. It critically depends on first achieving an optimal superposition of the two structures, a process that aligns them in three-dimensional space to minimize the measured deviations between equivalent atoms [21]. This preliminary alignment is essential for ensuring that the resulting RMSD value reflects genuine structural differences rather than arbitrary rotational or translational orientations. Without this optimal superposition, RMSD values are mathematically inflated and biologically meaningless, as they include the distances required to move one structure onto the other.

The importance of this metric extends far beyond simple structure comparison. It is fundamental for understanding protein function, elucidating evolutionary relationships, analyzing molecular dynamics simulations, and aiding in drug design by comparing ligand-bound and unbound conformations [21]. This application note details the core principles, key methodologies, and practical protocols for performing optimal superposition to calculate RMSD, providing researchers with the tools to apply this technique accurately in their work.

Fundamental Principles and Analytical Solutions

The Mathematical Foundation of RMSD

For two sets of corresponding points (e.g., C-alpha atoms) from two protein structures, designated as the mobile set (\mathbf{A} = {\mathbf{a}1, \mathbf{a}2, ..., \mathbf{a}N}) and the reference set (\mathbf{B} = {\mathbf{b}1, \mathbf{b}2, ..., \mathbf{b}N}), the RMSD is formally defined after a rigid-body transformation is applied to (\mathbf{A}). This transformation consists of a rotation matrix (R) and a translation vector (\mathbf{t}). The RMSD is given by the formula:

[ \text{RMSD}(R, \mathbf{t}) = \sqrt{\frac{1}{N}\sum{i=1}^{N} \| (R\mathbf{a}i + \mathbf{t}) - \mathbf{b}_i \|^2 } ]

The objective of optimal superposition is to find the specific rotation (R) and translation (\mathbf{t}) that globally minimize the value of this RMSD function [21]. The solution to this minimization problem is a well-established computational procedure.

The Kabsch Algorithm

The Kabsch algorithm provides an elegant, closed-form analytical solution to this minimization problem [21]. It is a deterministic and computationally efficient method that guarantees finding the optimal rotation and translation. The procedure follows these steps:

• Centering: Translate both the mobile set (\mathbf{A}) and the reference set (\mathbf{B}) so that their geometric centroids coincide at the origin of the coordinate system. This yields the centered coordinate sets (\mathbf{A}c) and (\mathbf{B}c), and solves for the optimal translation (\mathbf{t}) [21].
• Covariance Matrix Calculation: Compute the (3 \times 3) covariance matrix (\mathbf{H}) using the centered coordinates: (\mathbf{H} = \mathbf{A}c^T \mathbf{B}c) [21].
• Singular Value Decomposition (SVD): Perform SVD on the covariance matrix (\mathbf{H}), which decomposes it into three matrices: (\mathbf{H} = \mathbf{U} \Sigma \mathbf{V}^T) [21].
• Optimal Rotation Calculation: Calculate the optimal rotation matrix (R) as (R = \mathbf{V} \mathbf{U}^T). A critical check is performed on the determinant of (R) to ensure a proper rotation is obtained. If (\det(R) = -1), indicating a reflection, the sign of the last column of (\mathbf{V}) is inverted before recalculating (R) [21].

This algorithm serves as the gold standard for RMSD minimization and is embedded in countless structural bioinformatics software packages.

Advanced Superposition Frameworks

While the Kabsch algorithm is perfect for minimizing standard RMSD, modern computational challenges have spurred the development of more flexible frameworks.

A Gradient-Based Framework Using Lie Algebra

The Lie-RMSD framework reformulates the superposition problem to leverage modern gradient-based optimization [21]. Its key innovation is representing the rigid-body transformation (rotation and translation) as a single 6-dimensional vector in the Lie algebra (\mathfrak{se}(3)), which is the tangent space of the Special Euclidean group (SE(3)). This representation is fully differentiable, allowing the RMSD to be treated as a loss function that can be minimized by gradient-based optimizers like SGD, Adam, AdamW, and Sophia [21]. Although computationally more intensive than the analytical Kabsch solution, this framework's primary strength is its extensibility. It establishes a foundation for minimizing more complex, biologically relevant scoring functions (e.g., TM-score) that lack closed-form analytical solutions [21].

Handling Flexibility with Gaussian-Weighted RMSD

Standard RMSD is highly sensitive to outliers and local structural variations, such as flexible loops or hinged domain movements. To address this, the Gaussian-Weighted RMSD (wRMSD) method was developed [22]. Instead of selecting a subset of rigid residues, this method performs a superposition using all atoms. However, it assigns a weight to each atom based on its displacement between the two conformations. The weighting function ensures that atoms which move very little (the "static core") have a greater influence on the final superposition than atoms with large displacements [22]. This results in an alignment that better highlights the rigid-body relationship between two structures and the true range of flexibility in mobile regions.

Quantitative Benchmarking of Superposition Methods

The following table summarizes the performance of the Lie-RMSD framework, which uses gradient-based optimization, compared to the analytical Kabsch algorithm when aligning the allosteric conformations of Adenylate Kinase (PDB: 4AKE vs. 1AKE) [21].

Table 1: Benchmarking Results for Protein Structural Alignment (Adenylate Kinase)

Method	Final RMSD (Ã…)	Difference from Kabsch (Ã…)	Time (ms)
Kabsch (Ground Truth)	7.130699	—	0.51
Adam	7.130700	+0.000001	557.67
SGD	7.130702	+0.000003	549.55
Sophia	7.130710	+0.000011	587.31
AdamW	7.130717	+0.000018	582.88

The data shows that all gradient-based optimizers successfully converged to the global minimum found by the Kabsch algorithm, achieving effectively identical precision. The minor deviations are attributable to floating-point precision and iterative termination conditions [21]. The key trade-off is computational time, with the gradient-based methods taking three orders of magnitude longer than the analytical method for this specific task.

Experimental Protocols

Protocol 1: Basic RMSD Calculation Using the Kabsch Algorithm

This protocol provides a step-by-step guide for calculating the optimal RMSD between two protein structures with predefined atom correspondences.

Table 2: Research Reagent Solutions for Protocol 1

Item	Function/Description
C-alpha Atoms	Backbone atoms used to represent the protein fold; the most common choice for global structure comparison.
3D Coordinate Sets	The input data: two sets of Cartesian coordinates for the mobile (A) and reference (B) structures.
Computational Environment	A scripting environment (e.g., Python with NumPy/SciPy) capable of linear algebra operations, particularly SVD.

• Input Preparation:

  • Obtain the two protein structures (e.g., from PDB files).
  • Select equivalent atoms (e.g., C-alpha atoms for backbone comparison).
  • Ensure the two sets of coordinates (\mathbf{A}) and (\mathbf{B}) contain the same number of atoms (N) and are in the same sequential order.

• Centering (Optimal Translation):

  • Calculate the centroid for the mobile structure: (\text{centroid}A = \frac{1}{N}\sum{i=1}^{N} \mathbf{a}_i).
  • Calculate the centroid for the reference structure: (\text{centroid}B = \frac{1}{N}\sum{i=1}^{N} \mathbf{b}_i).
  • Center both sets by subtracting their respective centroids: (\mathbf{a}i^c = \mathbf{a}i - \text{centroid}A), (\mathbf{b}i^c = \mathbf{b}i - \text{centroid}B).

• Optimal Rotation via Kabsch Algorithm:

  • Compute the covariance matrix: (\mathbf{H} = (\mathbf{A}^c)^T \cdot \mathbf{B}^c).
  • Perform Singular Value Decomposition (SVD) on (\mathbf{H}): (\mathbf{U}, \Sigma, \mathbf{V}^T = \text{SVD}(\mathbf{H})).
  • Calculate the optimal rotation matrix: (R = \mathbf{V} \cdot \mathbf{U}^T).
  • Check for a reflection: if (\det(R) < 0), multiply the last column of (\mathbf{V}) by -1 and recalculate (R).

• Transformation and RMSD Calculation:

  • Apply the optimal transformation to the centered mobile coordinates: (\mathbf{A}^{\text{aligned}} = R \cdot \mathbf{A}^c + \text{centroid}_B).
  • Calculate the final RMSD: (\text{RMSD} = \sqrt{ \frac{1}{N} \sum{i=1}^{N} \| \mathbf{a}i^{\text{aligned}} - \mathbf{b}_i \|^2 }).

Protocol 2: Implementing the Lie-RMSD Framework

This protocol outlines the procedure for using the differentiable Lie-RMSD framework, which is particularly useful for testing custom loss functions [21].

• Initialization:

  • Represent the rigid-body transformation as a random or zero-initialized 6-dimensional vector (\mathbf{p} = (\boldsymbol{\omega}, \mathbf{u})) in (\mathfrak{se}(3)), where (\boldsymbol{\omega}) is rotation and (\mathbf{u}) is translation.
  • Center the coordinate sets (\mathbf{A}) and (\mathbf{B}) as described in Protocol 1.

• Optimization Loop:

  • Transformation: For the current parameters (\mathbf{p}), compute the rotation matrix (R) via the exponential map of the skew-symmetric matrix ([\boldsymbol{\omega}]_{\times}). Generate transformed coordinates: (\mathbf{A}^{\text{transformed}} = R(\boldsymbol{\omega}) \cdot \mathbf{A}^c + \mathbf{t}).
  • Loss Calculation: Compute the RMSD between (\mathbf{A}^{\text{transformed}}) and (\mathbf{B}^c), which serves as the loss function.
  • Gradient Calculation: Use automatic differentiation (e.g., in PyTorch) to compute the gradient of the loss with respect to the parameters (\mathbf{p}).
  • Parameter Update: Update the parameters (\mathbf{p}) using a gradient-based optimizer (e.g., Adam, SGD) for a specified number of steps or until convergence.

• Validation:

  • Validate the results by comparing the final RMSD and the superimposed structures against the output of the Kabsch algorithm.

The workflow below illustrates the logical relationship and decision path between the two protocols.

The Scientist's Toolkit

Table 3: Essential Software and Computational Tools for Protein Structural Alignment

Tool/Algorithm	Type	Primary Function in Superposition
Kabsch Algorithm [21]	Analytical Solution	Provides a closed-form, optimal solution for RMSD minimization.
Lie-RMSD [21]	Differentiable Framework	Represents superposition as a differentiable optimization problem for flexibility.
Gaussian-wRMSD [22]	Weighted Alignment	Performs superposition weighted by structural conservation, reducing noise from flexible regions.
TM-align [16]	Advanced Heuristic	Uses heuristic iteration and dynamic programming to maximize TM-score, a different similarity metric.
GraSR [23]	Alignment-Free ML	Uses Graph Neural Networks to learn structural representations, bypassing superposition for rapid retrieval.
SARST2 [16]	Database Search	Employs a filter-and-refine strategy with machine learning for rapid large-scale structural similarity searches.
Koreanoside G	Koreanoside G, MF:C24H26O11, MW:490.5 g/mol	Chemical Reagent
Torvoside D	Torvoside D, MF:C38H62O13, MW:726.9 g/mol	Chemical Reagent

Optimal superposition is not merely a preliminary step but the very foundation of a meaningful RMSD calculation. The Kabsch algorithm remains the gold standard for this task due to its precision and computational efficiency. However, emerging challenges in structural biology, such as the need to compare predicted models from AlphaFold DB and analyze flexible systems, demand more sophisticated tools [16] [22]. Modern frameworks like Lie-RMSD, which leverage automatic differentiation and Lie algebra, provide the flexibility to optimize beyond RMSD. Similarly, methods like wRMSD offer robust ways to handle conformational flexibility. As the volume of structural data continues to grow, the principles of optimal superposition will remain critical, even as they are embedded within faster, more powerful, and more biologically insightful structural comparison pipelines.

A Step-by-Step Guide to Calculating RMSD: From Theory to Practice

Root Mean Square Deviation (RMSD) is a fundamental metric in structural biology for quantifying the similarity between two molecular structures by measuring the average distance between equivalent atoms after optimal superposition [17]. It is extensively used to compare protein conformations, assess the quality of predicted models against experimental structures, and analyze conformational changes in molecular dynamics simulations [24] [17]. This guide provides a standardized, step-by-step protocol for calculating RMSD, enabling researchers to consistently perform and interpret this essential structural analysis.

Theoretical Foundation of RMSD

Mathematical Definition

The standard RMSD calculation involves a rigid-body superposition of two sets of equivalent atomic coordinates, followed by the computation of the average atomic displacement. For two sets of points, v and w, each containing n equivalent atoms, the RMSD is defined as [17]:

RMSD(v,w) = √( (1/n) × Σ ||vᵢ - wᵢ||² )

This equation calculates the square root of the mean squared distance between corresponding atoms after the structures have been optimally aligned. The most common atoms used for this calculation in proteins are the backbone atoms (N, Cα, C, O) or specifically the Cα atoms [24] [17].

Key Concepts in Superposition

A critical prerequisite for RMSD calculation is the optimal rigid-body transformation—comprising rotation and translation—that minimizes the RMSD between the two structures. This is typically solved using established algorithms like the Kabsch algorithm or quaternion-based methods [17]. It is crucial to distinguish between the atoms used for the superposition (the fitting set) and the atoms used for the final RMSD calculation, which can be identical or different. For instance, a structure is often fitted on the backbone atoms, but the RMSD can be computed for the backbone or the entire protein [24].

Computational Protocols

A Generalized Workflow for RMSD Calculation

The following diagram outlines the core steps for calculating RMSD between two protein structures, from data preparation to interpretation.

Step-by-Step Procedure

Step 1: Input Structure Preparation

• Obtain Structures: Acquire 3D atomic coordinates in PDB or mmCIF format from sources like the Protein Data Bank (PDB) or homology modeling servers (e.g., SWISS-MODEL, AlphaFold) [10] [25].
• Select Chains and Residues: Specify the polymer chain(s) and residue ranges for comparison. The selected chain must be at least 10 residues long and contain coordinates for Cα atoms [10].
• Curate Atoms: Remove heteroatoms (water, ligands) and select relevant atoms for analysis (e.g., protein backbone, Cα only, or all atoms).

Step 2: Atom Selection and Correspondence

• Define Equivalent Atoms: Establish a residue-to-residue correspondence, which can be sequence-dependent (sequential) or independent (non-sequential) [26] [10].
• Choose Atom Set: Select the atomic coordinates for calculation. Using only Cα atoms is common for a global backbone comparison.

Step 3: Structural Superposition

• Center Structures: Translate both structures so their geometric centers (centroids) coincide at the origin.
• Compute Optimal Rotation: Apply the Kabsch algorithm to find the rotation matrix that minimizes the RMSD between the two coordinate sets [17].

Step 4: RMSD Computation

• Apply Transformation: Rotate the target structure using the optimal rotation matrix.
• Compute the Final Value: Use the standard RMSD formula to calculate the value, typically reported in Ã…ngströms (Ã…).

Selecting an Appropriate Algorithm

Different alignment algorithms are suited for different scenarios. The table below summarizes common methods available through the RCSB PDB Pairwise Structure Alignment tool [10].

Table 1: Common Structural Alignment Algorithms for RMSD Calculation

Algorithm	Alignment Type	Key Features	Best Used For
jFATCAT-rigid [10]	Rigid-body	Identifies largest structurally conserved core; sequence-order dependent.	Comparing closely related proteins with minimal conformational changes.
jFATCAT-flexible [10]	Flexible	Introduces twists (hinges) to align rigid domains independently.	Comparing proteins with large internal conformational changes (e.g., upon ligand binding).
jCE [10]	Rigid-body	Combines similar local structure segments to maximize aligned residues.	General-purpose, sequence-order dependent alignment of globular proteins.
jCE-CP [10]	Flexible	Allows for circular permutations and different loop topologies.	Comparing proteins with similar shapes but different backbone connectivity.
TM-align [10]	Rigid-body	Sequence-independent; sensitive to global topology.	Comparing proteins with similar folds, even with low sequence similarity.

Research Reagent Solutions

A successful RMSD analysis relies on both reliable data and robust software tools.

Table 2: Essential Resources for Protein Structure Comparison and RMSD Calculation

Resource Category	Example	Function and Utility
Structure Databases	Protein Data Bank (PDB) [10]	Primary repository for experimentally determined 3D structures of proteins and nucleic acids.
Homology Modeling Servers	SWISS-MODEL [25]	Fully automated protein structure homology-modelling server for generating 3D models from amino acid sequences.
Predicted Structure Databases	AlphaFold DB [10] [25]	Database of highly accurate predicted protein structures generated by AlphaFold2, accessible as templates or for direct comparison.
Structure Alignment Tools	RCSB PDB Pairwise Structure Alignment [10]	Web-accessible interface providing multiple algorithms (jFATCAT, jCE, TM-align) for structural superposition and RMSD calculation.
Standalone Software	GROMACS (gmx rms) [24]	Molecular dynamics package with built-in tools for calculating RMSD, including least-squares fitting and fit-free methods.

Data Interpretation and Reporting

Interpreting RMSD Values

The absolute RMSD value provides a quantitative measure of structural similarity. Lower values indicate higher similarity. As a general guideline:

• RMSD < 1.0 - 2.0 Ã…: Often considered a high-quality match for closely related proteins or accurate model predictions, especially when superimposed on stable core regions [27] [28].
• RMSD ~ 2.0 - 4.0 Ã…: Typical for structures with the same overall fold but some structural variations, such as loop movements or differences between bound and unbound forms.
• RMSD > 4.0 Ã…: May suggest different folds or significant structural rearrangements, though contextual factors like the length and flexibility of the aligned region must be considered.

Complementary Metrics

While RMSD is a standard measure, it is sensitive to local errors and can be dominated by a small subset of poorly aligned residues. Reporting complementary metrics provides a more comprehensive assessment [10]:

• TM-score: A topology-based measure that is less sensitive to local variations. A score >0.5 generally indicates the same protein fold, while a score <0.2 suggests unrelated structures [10].
• Sequence Identity: The percentage of identical residues in the structural alignment.
• Number of Equivalent Residues: The count of residue pairs deemed structurally equivalent by the alignment algorithm.

Application Notes

Example: Benchmarking Model Accuracy

A primary application of RMSD is validating computationally predicted protein structures. For instance, the Protein Models Docking Benchmark 2 was created by generating protein models with Cα RMSD to native structures in the 1 to 6 Å range, providing a standardized set for testing docking methods [27]. In such a benchmark:

• Procedure: Generate a 3D model of a protein with a known experimental structure (the "native" or "target").
• Alignment: Superimpose the model onto the native structure using a rigid-body alignment on all Cα atoms.
• Calculation: Compute the Cα RMSD for the entire chain or a specific domain.
• Interpretation: A lower global Cα RMSD typically indicates a more accurate model, with values below ~2 Ã… often considered high-quality for the core structural regions [27].

Troubleshooting Common Issues

• High RMSD Due to Flexible Regions: If a structure has highly flexible termini or loops, they can disproportionately inflate the RMSD. Consider calculating RMSD only on well-structured core regions.
• Effect of Alignment Size: The RMSD value is influenced by the number of atoms included. Always report the number of equivalent residues used in the calculation for context [10].
• Choice of Reference Atoms: Be consistent in the atoms selected for comparison (e.g., always Cα or always backbone) across different analyses to ensure results are comparable.

Root Mean Square Deviation (RMSD) is a fundamental metric in structural biology and computational chemistry, providing a quantitative measure of the average distance between the atoms of two superimposed molecular structures [2]. The calculation of RMSD is a critical step in numerous research applications, including the analysis of protein conformational changes, validation of predicted protein models against experimental structures, assessment of molecular dynamics (MD) simulation trajectories, and evaluation of docking poses in drug design [2] [3]. The mathematical formula for RMSD is expressed as the square root of the average of the squared distances between corresponding atoms: RMSD = √[ (1/N) * Σ(d_i)² ], where N is the number of atoms, and d_i is the distance between the i-th pair of corresponding atoms [3] [29].

However, a raw RMSD calculation can be misleading unless the structures are optimally superimposed to minimize the influence of overall translation and rotation in 3D space [30] [31]. Furthermore, challenges such as differing atom ordering between structure files or the presence of symmetric atoms in ligands can artificially inflate RMSD values if not properly addressed [29]. Consequently, the choice of software is paramount, as robust tools automatically perform necessary pre-processing steps—including structural alignment, atom mapping, and symmetry correction—to ensure the resulting RMSD value accurately reflects genuine structural differences [30] [29]. This application note provides a structured overview of available software and servers, detailed protocols, and data interpretation guidelines to empower researchers in selecting the appropriate tool for their specific research context.

Key Considerations and Limitations of RMSD

Before selecting a tool, researchers must understand both the power and the limitations of the RMSD measure. A significant drawback of global RMSD is its sensitivity to outliers; it is dominated by the largest deviations in the structure [3]. For instance, a single flexible loop or terminal region with high conformational freedom can disproportionately increase the global RMSD, masking a high degree of similarity in the structural core [3]. This makes global RMSD a potentially poor indicator of overall structural similarity, especially for flexible proteins or multi-domain proteins with relative domain movements.

To address this, researchers often employ alternative strategies. Local RMSD analysis can be performed on specific regions of interest, such as a binding pocket or a protein domain, to focus on functionally relevant areas [3]. Additionally, alternative metrics have been developed. Template Modeling Score (TM-score) and MaxSub are two such measures that are less sensitive to local errors because they are designed to identify the largest subset of residues that can be superimposed within a defined distance threshold [32]. The TM-score is particularly valuable as it is normalized by protein length, providing a more universal scale where a score above 0.5 generally indicates the same fold, and a score below 0.17 corresponds to random similarity [32].

Another critical consideration is molecular symmetry. For symmetric molecules, such as benzene or ibuprofen, multiple, chemically equivalent atomic mappings are possible [29]. A naïve RMSD calculation that relies on the atom order in the input files can yield an artificially high value. Specialized tools like DockRMSD are essential in these scenarios, as they solve the graph isomorphism problem to find the minimal RMSD based on all possible physically allowed atomic mappings that respect the molecular bonding network [29].

Table 1: Interpretation Guidelines for RMSD and Alternative Metrics

Metric	Typical Range for Similar Structures	Interpretation and Notes
Global Cα RMSD	0 - 1.2 Å [3]	Values in this range often reflect inherent protein flexibility or minor experimental differences. Values > 2-3 Å typically indicate significant conformational changes or potential alignment issues [2] [3].
Local RMSD	Varies by region	Focuses on a specific functional site (e.g., active site). Useful for docking validation when global RMSD is high due to flexible regions.
TM-score	0.5 - 1.0 [32]	A score > 0.5 indicates the same fold; < 0.17 suggests random similarity. Length-normalized and more robust to local errors than RMSD.
MaxSub Score	0.0 - 1.0 [32]	Identifies the largest subset of residues fitting under a distance cutoff. A value of 1 indicates an identical pair of structures.

Software and Server Toolkit for RMSD Calculation

A wide array of tools is available for calculating RMSD, ranging from simple command-line scripts to complex visualization suites with integrated analysis. The choice depends on the user's specific task, such as comparing a few structures versus processing thousands, or working with simple proteins versus symmetric small molecules.

Table 2: Software Toolkit for RMSD Calculation

Tool Name	Primary Use Case & Description	Key Features	Format Support
rmsd (Python) [30] [31]	Command-line tool for fast, optimal RMSD. Ideal for batch processing and scripts.	Handles translation/rotation; atom reordering; ignores hydrogens.	.xyz, .pdb
DockRMSD [29]	Specialized for symmetric ligands in docking poses. Critical for drug development.	Graph isomorphism for physical atom mapping; deterministic minimal RMSD.	.mol2
MaxCluster [32]	Protein-specific comparison & clustering. Excellent for large-scale model assessment.	RMSD, TM-score, MaxSub; sequence-dependent/independent alignment; clustering.	.pdb
Visualization Suites (VMD, PyMOL, ChimeraX) [2] [33]	Interactive analysis with visualization. Perfect for validating alignments and results.	GUI-based calculation; visual inspection of superpositions; scripting for automation.	.pdb, .xyz, etc.
MD Suites (GROMACS, NAMD) [33] [34]	Integrated analysis of molecular dynamics trajectories.	Calculates RMSD over time with automatic least-squares fitting to remove rotation/translation [34].	Trajectory formats
Valeriotriate B	Valeriotriate B, MF:C27H42O12, MW:558.6 g/mol	Chemical Reagent	Bench Chemicals
Crovatin	Crovatin, MF:C21H26O6, MW:374.4 g/mol	Chemical Reagent	Bench Chemicals

The following diagram illustrates the decision-making workflow for selecting the most appropriate RMSD calculation tool based on your research objectives.

Detailed Protocols for Common Research Scenarios

Protocol 1: Calculating RMSD for a Symmetric Ligand with DockRMSD

Research Context: This protocol is essential in drug development for accurately evaluating docking poses of symmetric small molecule ligands, where naive RMSD can be misleading [29].

Experimental Workflow:

• Input Preparation: Prepare two ligand structure files in MOL2 format. One is the reference (e.g., the crystallographic pose), and the other is the query (e.g., the docked pose). Ensure the files correctly specify atom elements, 3D coordinates, and the bonding network.
• Software Acquisition: Download the open-source DockRMSD program from its official website [29]. Compile the C source code or use the provided binaries.
• Execution: Run the calculation from the command line. A basic command is: DockRMSD -q query_structure.mol2 -t template_structure.mol2 This command will output the symmetry-corrected minimal RMSD value.
• Validation: Visually inspect the aligned structures in a molecular viewer to confirm the atomic mapping is chemically sensible. DockRMSD ensures this by using graph isomorphism that respects the bonding structure [29].

Protocol 2: Large-Scale Comparison of Protein Models with MaxCluster

Research Context: This protocol is used in community-wide assessments like CASP and for benchmarking protein structure prediction methods against experimental answers by comparing thousands of models [3] [32].

Experimental Workflow:

• Input Preparation: Collect all protein models and the reference experimental structure in PDB format.
• Software Acquisition: Download the MaxCluster command-line tool from the official site [32].
• Execution:
  • For a single model against a reference: MaxCluster -s 1 reference.pdb model.pdb
  • For an all-versus-all comparison of multiple models: MaxCluster -a -l list_of_models.txt The -s 1 option performs a sequence-dependent alignment and reports RMSD, among other scores.
• Output Analysis: MaxCluster generates a table of scores. For a comprehensive assessment, consider not only RMSD but also the TM-score, which provides a more robust evaluation of the overall fold similarity [32].

Protocol 3: Analyzing RMSD from a GROMACS MD Trajectory

Research Context: This protocol is standard in molecular dynamics simulations to monitor the stability of a protein or polymer backbone by measuring its structural evolution relative to a starting frame [34].

Experimental Workflow:

• Trajectory Preparation: Use gmx trjconv to correct for periodic boundary conditions (PBC) and center the system, outputting a trajectory that contains only the molecule of interest (e.g., a polymer chain).
• Index Group Creation: Use gmx make_ndx to create index groups for the specific parts you wish to analyze (e.g., "Backbone" and "Sidechains").
• RMSD Calculation: Use the gmx rms tool to compute the RMSD. The command automatically performs a least-squares fit to remove overall translation and rotation before calculating the deviation [34]. An example command is: gmx rms -s reference.tpr -f trajectory.xtc -o rmsd_backbone.xvg -n index.ndx When prompted, select your "Backbone" index group for both the fitting and the calculation.
• Plotting and Interpretation: The output .xvg file can be plotted to visualize RMSD over time. Initial increases often indicate equilibration, while a stable plateau suggests conformational stability [34].

The Scientist's Toolkit: Essential Research Reagents and Materials

Table 3: Essential "Reagents" for Computational RMSD Analysis

Item / Resource	Function in RMSD Analysis
Protein Data Bank (PDB) File	The standard format for storing experimental 3D structures of biological macromolecules. Serves as the primary input and reference for comparison.
Molecular Dynamics Trajectory File	A series of molecular structures over time (e.g., in .xtc, .dcd format). The input for analyzing conformational stability and changes during simulation.
Index File (e.g., GROMACS .ndx)	Defines groups of atoms for targeted analysis (e.g., "Backbone", "Sidechains", "Binding Site"). Allows for localized RMSD calculation.
AlphaFold Protein Structure Database [35]	A repository of over 200 million predicted protein structures. Provides high-accuracy models that can be used as references when experimental structures are unavailable.
Command-Line Interface (Shell)	The environment for executing most high-performance computational tools (e.g., rmsd, MaxCluster, GROMACS). Essential for automation and batch processing.

Implementing the Kabsch Algorithm for Optimal Rigid-Body Superposition

The comparison of three-dimensional protein structures is a fundamental task in structural biology, bioinformatics, and drug development. The Root Mean Square Deviation (RMSD) of atomic positions serves as a principal quantitative metric for assessing structural similarity between two protein conformations or models. The Kabsch algorithm provides an elegant, closed-form solution to the problem of finding the optimal rotation matrix that minimizes the RMSD between two paired sets of points, thus enabling meaningful structural comparisons. This algorithm has become the gold standard for rigid-body superposition in structural biology due to its computational efficiency and mathematical robustness. Within the broader context of protein structure comparison research, accurate RMSD calculation forms the foundation for evaluating protein folding simulations, assessing computational models against experimental structures, classifying structural similarities, and understanding conformational changes relevant to drug binding. This protocol details the implementation and application of the Kabsch algorithm specifically for protein structure comparison, providing researchers with a standardized methodology for rigorous structural analysis.

Theoretical Foundation

Root Mean Square Deviation (RMSD) in Structural Biology

The Root Mean Square Deviation measures the average distance between atoms of superimposed macromolecules, most commonly calculated for backbone atoms or Cα atomic coordinates after optimal rigid body superposition. The RMSD between two sets of coordinates is mathematically defined as:

RMSD = √[ (1/N) × Σ(δ_i)² ]

where δ_i represents the distance between atom i in the two structures after superposition, and N is the total number of atoms compared. The RMSD value is expressed in Ångströms (Å), with lower values indicating higher structural similarity. In protein structure comparison, RMSD provides a single summary metric that quantifies global structural differences, making it invaluable for assessing model accuracy in initiatives like CASP (Critical Assessment of protein Structure Prediction) and for analyzing conformational changes in molecular dynamics simulations. However, RMSD has recognized limitations: it is highly sensitive to local structural variations and outliers, particularly flexible loops or termini, and can be dominated by the largest errors in a structure, potentially obscuring local regions of high similarity.

Mathematical Principles of the Kabsch Algorithm

The Kabsch algorithm addresses the fundamental challenge in RMSD calculation: finding the optimal rotation and translation that minimizes the RMSD between two paired sets of points. Given two sets of points P and Q, each containing N points in three-dimensional space representing atomic coordinates, the algorithm computes the optimal rotation matrix R and translation vector that minimizes the RMSD. The algorithm operates through a sequence of linear algebra operations beginning with centroid calculation and culminating in singular value decomposition (SVD). The power of the algorithm lies in its ability to efficiently determine the global minimum RMSD without iterative approximation, providing an exact solution to the rigid-body superposition problem. This mathematical foundation ensures that researchers obtain consistent, reproducible alignments for structural comparison.

Methodology

Kabsch Algorithm Step-by-Step Protocol

Centroid Calculation and Centering

The initial step involves translating both structures to their geometric center at the origin of the coordinate system. This removes the translational component, allowing subsequent steps to focus on determining the optimal rotation.

• Calculate the centroid (geometric center) for each set of points:

  • Centroid of P: μP = (1/N) × Σpi
  • Centroid of Q: μQ = (1/N) × Σqi where pi and qi represent the coordinates of point i in structures P and Q respectively.

• Center both point sets by subtracting their respective centroids:

  • Pcentered = P - μP
  • Qcentered = Q - μQ

This centering step simplifies subsequent calculations by ensuring both structures are positioned around the origin, making the algorithm independent of the initial positions of the structures.

Covariance Matrix Computation

Compute the 3×3 cross-covariance matrix H that captures the relationship between the centered point sets:

H = (Pcentered)^T × Qcentered

In summation notation, each element of the matrix is calculated as: Hij = Σ[(Pcentered)ki × (Qcentered)_kj] for k = 1 to N

This covariance matrix encapsulates the mutual variations between the two point sets and is crucial for determining their optimal alignment.

Singular Value Decomposition (SVD)

Perform singular value decomposition (SVD) on the covariance matrix H:

H = U × Σ × V^T

where U and V are orthogonal matrices containing the left and right singular vectors, and Σ is a diagonal matrix containing the singular values of H. The SVD effectively decomposes the transformation between the two point sets into fundamental components: rotation, scaling, and another rotation.

Optimal Rotation Matrix Calculation

Calculate the optimal rotation matrix R using the components from SVD:

R = V × U^T

A critical check must be performed to ensure this represents a proper rotation (not a reflection). If the determinant of R is negative (det(R) < 0), reflection is detected and corrected by negating the third column of V before recalculating R:

if det(R) < 0: V[:,2] = -V[:,2] R = V × U^T

This adjustment ensures the algorithm produces a proper rotation matrix with determinant +1.

RMSD Calculation and Structure Alignment

With the optimal rotation determined, the final RMSD can be calculated and the structures aligned:

• Align structure Q to P: Qaligned = (Q - μQ) × R + μ_P

• Calculate the minimum RMSD: RMSD = √[ (1/N) × Σ ||(R × (qi - μQ) + μP) - pi||² ]

The algorithm ensures that this RMSD value represents the global minimum achievable through rigid-body transformation.

Workflow Visualization

Figure 1: Kabsch Algorithm Workflow. This diagram illustrates the sequential steps for implementing the Kabsch algorithm for protein structure alignment.

Python Implementation

The following Python code implements the Kabsch algorithm for protein structure comparison:

This implementation provides a complete, functional implementation of the Kabsch algorithm that can be directly applied to protein coordinate data. The function returns the optimal rotation matrix, translation vector, and minimized RMSD value.

Advanced Implementation Considerations

Handling Special Cases and Numerical Stability

In practical applications, several special cases require careful handling to ensure algorithm robustness:

• Collinear points: When atoms are perfectly collinear, the covariance matrix becomes singular. Implementing quaternion-based solutions can provide an alternative approach in these rare cases.

• Numerical precision: For large structures with many atoms, accumulated floating-point errors can affect results. Using double-precision arithmetic and validating with known test cases mitigates this issue.

• Identical structures: When P and Q are identical, the algorithm should return an identity rotation matrix and zero RMSD. Including validation tests for this case ensures implementation correctness.

• Weighted superposition: Advanced applications may require weighting atoms differently based on confidence measures or atom type. This requires modifying the centroid and covariance calculations to incorporate weights.

Kabsch-Umeyama Variant with Scaling

For applications requiring uniform scaling in addition to rotation and translation, the Kabsch-Umeyama variant provides an extended solution:

This variant is particularly useful when comparing structures that may have undergone uniform expansion or contraction.

Applications in Protein Structure Research

Comparative Protein Structure Analysis

The Kabsch algorithm enables multiple critical applications in structural biology:

• Model validation: Comparing computational models to experimental reference structures in assessments like CASP and GPCR Dock.

• Conformational analysis: Quantifying structural changes between different functional states of proteins, such as open and closed conformations.

• Molecular dynamics: Tracking structural evolution during simulation trajectories by calculating RMSD relative to initial or reference structures.

• Drug discovery: Superposing protein-ligand complexes to identify conserved binding modes and structural motifs.

• Evolutionary studies: Quantifying structural similarity between homologous proteins to infer functional relationships.

Comparison with Alternative Approaches

Table 1: Protein Structure Comparison Methods

Method	Type	Optimization Target	Advantages	Limitations
Kabsch Algorithm	Analytical	RMSD minimization	Exact solution, computationally efficient, mathematically elegant	Requires predefined atom correspondence, sensitive to outliers
Quaternion Method	Analytical	RMSD minimization	Numerically stable, avoids reflection issues	Less intuitive implementation
Lie-RMSD	Gradient-based	RMSD minimization	Flexible framework for custom loss functions	Iterative, potentially slower convergence
TM-align	Heuristic	TM-score maximization	More robust to structural outliers	No analytical solution, heuristic approach
DALI	Search-based	Z-score optimization	Sequence-independent alignment	Computationally intensive for large databases

Performance Benchmarking

Table 2: Performance Comparison of Structural Alignment Methods

Method	Algorithm Type	RMSD Precision (Ã…)	Computational Time	Typical Use Cases
Kabsch	Analytical	Exact to machine precision	~0.5 ms for 200 atoms	Rigid-body superposition, dynamics analysis
Lie-RMSD (Adam)	Gradient-based	±0.000001 Å	~550 ms	Flexible framework development
GTalign-web	Spatial indexing	N/A	~34 min (100 queries)	Large database searches
DALI	Search-based	N/A	~477 min (100 queries)	Structural homology detection

Recent benchmarking studies demonstrate that the Kabsch algorithm remains the most efficient method for RMSD minimization when atom correspondence is known. In a comparison of alignment methods for the allosteric transition of Adenylate Kinase (PDB: 4AKE vs 1AKE), the Kabsch algorithm achieved an RMSD of 7.130699 Ã… in approximately 0.51 milliseconds, outperforming gradient-based approaches in both speed and precision.

Research Reagent Solutions

Table 3: Essential Computational Tools for Protein Structure Analysis

Tool/Resource	Function	Application in Research
NumPy	Numerical computing library	Matrix operations for Kabsch implementation
BioPython	Biological data manipulation	PDB file parsing and structure representation
PyMOL	Molecular visualization	Visual validation of structural alignments
CHARMM	Molecular simulation	Dynamics simulations and trajectory analysis
GTalign-web	Web-based structure alignment	Large-scale structural comparisons
RCSB PDB	Structure database	Source of experimental reference structures
DALI Server	Structure similarity search	Detection of structural homologs
Foldseek	Fast structure search	Efficient database scanning

Experimental Protocol

Practical Workflow for Protein Structure Comparison

Data Preparation and Preprocessing

• Structure retrieval: Obtain protein structures in PDB format from the RCSB Protein Data Bank or similar repositories.

• Atom selection: Extract relevant atoms for comparison, typically Cα atoms for backbone comparison or specific residues for binding site analysis.

• Coordinate extraction: Parse PDB files to obtain atomic coordinates as N×3 matrices, where N represents the number of equivalent atoms in both structures.

• Sequence alignment: Ensure proper residue correspondence between structures using sequence alignment tools such as BLAST or structural alignment methods when sequences diverge.

Implementation and Validation

• Algorithm implementation: Code the Kabsch algorithm following the provided Python implementation, ensuring proper handling of special cases.

• Validation with known structures: Test the implementation using structures with known relationships, such as different conformations of the same protein.

• Visual verification: Use molecular visualization software (e.g., PyMOL, Chimera) to visually inspect the quality of structural superpositions.

• Benchmarking: Compare results against established tools to verify implementation correctness.

Analysis and Interpretation

• RMSD calculation: Compute the minimized RMSD value for the optimally aligned structures.

• Region-specific analysis: Calculate local RMSD values for specific structural domains or functional sites to identify regions of high conservation or variability.

• Statistical context: Interpret RMSD values in the context of known structural variations. For example, RMSD values below 1.0-1.5 Ã… typically indicate highly similar structures, while values above 2.5-3.0 Ã… suggest significant conformational differences.

• Complementary metrics: Supplement RMSD analysis with other similarity measures such as TM-score or GDT_TS for a more comprehensive assessment of structural similarity.

Algorithm Structure and Data Flow

Figure 2: Protein Structure Analysis Pipeline. This diagram illustrates the complete workflow from data input to analytical application in protein structure research.

The Kabsch algorithm provides an efficient, mathematically rigorous method for determining the optimal rigid-body transformation that minimizes RMSD between protein structures. Its closed-form solution based on singular value decomposition ensures computational efficiency and precision, making it ideal for applications ranging from model validation to conformational analysis. When implemented following the detailed protocol outlined in this document, researchers can reliably compare protein structures and quantify their similarities and differences. While RMSD has known limitations as a global metric, its minimization via the Kabsch algorithm remains a fundamental operation in structural bioinformatics. The continued relevance of this algorithm is evidenced by its integration into major structural analysis packages and its role as a benchmark for emerging methods such as gradient-based Lie algebra approaches. For protein structure researchers, mastery of this algorithm provides an essential tool for rigorous structural comparison and analysis.

Sequence-Dependent vs. Sequence-Independent Alignment Methods

Quantifying the similarity between three-dimensional protein structures is a fundamental task in structural biology, with critical applications in evolutionary studies, protein function annotation, and drug development. The root mean square deviation (RMSD) of atomic positions serves as a principal metric for this purpose, measuring the average distance between atoms of superimposed protein structures [17]. The calculation of a meaningful RMSD, however, is contingent upon a critical preliminary step: determining the correspondence between residues in the two structures being compared. This establishes two principal methodological frameworks—sequence-dependent and sequence-independent alignment—which dictate how residue equivalences are defined and significantly influence the resulting structural similarity assessment [3].

Core Conceptual Differences

The distinction between sequence-dependent and sequence-independent methods lies in their approach to establishing residue correspondence.

Sequence-dependent methods assume a strict one-to-one correspondence between target and model residues based on their sequence order [3]. This approach directly maps the i-th residue of one structure to the i-th residue of the other, relying on their identical sequential positions. The alignment is thus constrained by the amino acid sequence alignment.

Sequence-independent methods perform structural superimposition first, then evaluate residue correspondence based on spatial proximity after optimal rigid-body superposition [3]. These methods identify structurally equivalent residues regardless of their sequence order, allowing for detection of structural similarity even when sequence threading within the fold is incorrect.

Table 1: Fundamental Characteristics of Alignment Methods

Feature	Sequence-Dependent Alignment	Sequence-Independent Alignment
Residue Correspondence	Strict one-to-one based on sequence order	Determined by spatial proximity after structural superposition
Sequence Requirement	Requires identical sequence length and order	Accommodates different sequence lengths and orders
Primary Application	Comparing structures of identical or highly similar sequences	Detecting structural similarity in distantly related proteins or analogous folds
Sensitivity to Domain Rearrangements	Low sensitivity	High sensitivity
Influence on RMSD	RMSD reflects deviations from expected sequence positions	RMSD reflects pure spatial deviations of structurally equivalent regions

Quantitative Comparison and Performance Metrics

The choice between sequence-dependent and sequence-independent approaches significantly impacts RMSD values and structural similarity assessments. Sequence-independent methods generally identify larger sets of equivalent residues but may yield higher RMSD values due to inclusion of more distant regions.

Table 2: Performance Comparison of Alignment Methods

Metric	Sequence-Dependent	Sequence-Independent
Alignment Accuracy	High for sequence-similar proteins (>90% identity)	Superior for proteins with <40% sequence identity [3]
Residue Coverage	Fixed to full sequence length	Variable, typically identifies common structural cores
Robustness to Errors	Sensitive to sequence alignment errors	More robust to local structural variations
Computational Complexity	Generally lower	Higher due to search for optimal correspondence
Detection of Non-Sequential Similarity	Limited capability	Can detect structural mimicry and analogous folds [36]

The normalized RMSD (nRMSD) has been developed to facilitate comparison across proteins of different sizes. The traditional RMSD depends on protein dimension (number of equivalent atom pairs), making values for different-sized proteins incomparable. The nRMSD applies a normalization procedure to create a size-independent metric, which is particularly valuable in evolutionary and fold classification studies [5].

Experimental Protocols

Protocol for Sequence-Dependent RMSD Calculation

This protocol is ideal for comparing alternative conformations of the same protein or validating computational models against experimental structures when sequence identity is high.

• Input Structure Preparation: Obtain protein structures in PDB format. Ensure sequences are identical in length and residue order.
• Atom Selection: Select equivalent atom sets (typically Cα atoms for backbone comparison or all heavy atoms for full-structure assessment).
• Sequence Alignment: Perform optimal sequence alignment using algorithms such as Needleman-Wunsch for global alignment [37] [38].
• Rigid-Body Superposition: Apply the Kabsch algorithm to perform optimal rotation and translation that minimizes the RMSD between pre-defined equivalent atoms [17].
• RMSD Calculation: Compute the metric using the formula: RMSD = √(1/n × Σ(d_i²)) where n is the number of atom pairs and d_i is the distance between the i-th pair of equivalent atoms after superposition [17].
• Validation: Compare calculated RMSD against established thresholds (e.g., <1-2 Ã… for high accuracy, 2-4 Ã… for medium accuracy).

Protocol for Sequence-Independent RMSD Calculation

This protocol is suitable for detecting structural similarities between distantly related proteins or proteins with suspected non-sequential structural relationships.

• Input Structure Preparation: Obtain protein structures in PDB format. No requirement for identical sequence length or order.
• Structural Superposition: Use sequence-independent alignment algorithms (e.g., LGA, CE, DALI, SSM, US-align2) to identify structurally equivalent regions [3] [36].
• Equivalent Atom Identification: Based on spatial proximity after superposition, identify residue pairs where Cα atoms fall within a defined cutoff distance (typically 3.5-4.0 Ã…).
• Core Structure Extraction: Select the largest set of equivalenced residues that form a structurally conserved core.
• RMSD Calculation: Compute RMSD using the standard formula but applied only to the identified equivalent atom pairs from the structural alignment.
• Alternative Metrics Calculation: Supplement RMSD with additional metrics such as Global Distance Test (GDT) scores or Template Modeling Score (TM-score) for more comprehensive assessment [17].

Workflow Visualization

Structural Alignment Decision Workflow

Table 3: Key Software Tools for Structural Alignment and RMSD Calculation

Tool Name	Alignment Type	Primary Function	Application Context
US-align2 [36]	Both sequential and non-sequential	Unified protein and nucleic acid structure alignment	Detection of structural mimicry and distant relationships
LGA (Local-Global Alignment) [3]	Primarily sequence-independent	Superimposition and model evaluation	CASP assessments; identification of structural cores
Kabsch Algorithm [17]	Implementation dependent	Optimal rigid-body superposition	Core mathematics behind many superposition tools
DockRMSD [29]	Specialized for symmetric molecules	Symmetry-corrected RMSD calculation	Ligand docking pose evaluation
LSQMAN [3]	Sequence-independent	Structural comparison and analysis	Handling structural rearrangements and domain movements
CE (Combinatorial Extension) [3]	Sequence-independent	Protein structure alignment	Detecting distant structural similarities
DALI [3]	Sequence-independent	Protein structure comparison	Database searching and fold classification

Application Guidelines and Decision Framework

The choice between sequence-dependent and sequence-independent methods should be guided by research goals and sequence characteristics:

• Use Sequence-Dependent Methods When: Comparing structures of the same protein (e.g., molecular dynamics trajectories, mutant analyses, computational model validation), when sequences share >90% identity, or when assessing global conformational changes while maintaining sequence register [3] [38].

• Use Sequence-Independent Methods When: Analyzing distantly related proteins with sequence identity <40%, detecting structural similarities despite different fold topologies, identifying structural motifs or binding sites, or when proteins exhibit circular permutations or domain swapping [3] [36].

For novel protein structures with unknown relationships, a hierarchical approach is recommended: begin with sequence-independent methods to detect any structural similarity, then apply sequence-dependent analysis if high sequence similarity is confirmed.

Advanced Considerations and Limitations

While RMSD remains a widely used metric, it has recognized limitations. The measure is dominated by the largest errors in the structure, meaning that a single deviating region can disproportionately inflate the RMSD value, potentially masking high similarity in other regions [3]. This has led to the development of complementary metrics such as Global Distance Test (GDT) and Template Modeling (TM) scores, which provide more robust assessments of overall structural similarity [17].

Recent advancements in machine learning-based structure prediction, particularly AlphaFold2 and AlphaFold3, have transformed the field. These tools achieve remarkable accuracy (AlphaFold2 reported backbone RMSD of 0.8 Ã… compared to experimental structures) and utilize sophisticated internal representations of structural relationships that transcend simple sequence-based correspondence [39]. Nevertheless, traditional RMSD calculations remain essential for validating these predictions and quantifying structural differences in both academic research and drug development pipelines.

Root Mean Square Deviation (RMSD) is a fundamental metric in structural bioinformatics and computer-aided drug design, providing a quantitative measure of the average distance between atoms in superimposed molecular structures [17]. In protein-ligand docking, RMSD calculations are crucial for evaluating how closely a predicted binding pose matches a known experimental structure, thereby benchmarking docking algorithm performance [29] [40]. The standard RMSD calculation assumes direct atomic correspondence between structures, where atom i in one structure is compared to atom i in another structure [41]. This assumption holds for asymmetric molecules but fails dramatically for symmetric molecules, leading to artificially inflated RMSD values that inaccurately represent pose similarity [29] [40]. For symmetric molecules like benzene or ibuprofen, chemically identical binding poses can yield unexpectedly high RMSD values due to arbitrary atomic labeling differences rather than genuine structural differences [29]. This review addresses the critical challenge of symmetry-corrected RMSD calculation for ligands, focusing on specialized tools like DockRMSD that implement graph isomorphism approaches to determine chemically relevant atomic mappings.

The Fundamental Problem: Molecular Symmetry and RMSD Artifacts

Limitations of Standard RMSD Calculations

The standard RMSD formula is defined as:

[ RMSD = \sqrt{\frac{1}{N}\sum{i=1}^{N}\deltai^2} ]

where N represents the number of atoms, and δ_i is the distance between atom i in the reference structure and its corresponding atom in the compared structure [17]. For symmetric molecules, this direct correspondence breaks down because multiple, chemically equivalent atomic mappings exist. For example, a 180-degree rotation of a benzene ring around its symmetry axis produces a chemically identical configuration, but standard RMSD calculations would report a substantial deviation due to different atom labels occupying the same spatial positions [29]. This artifact presents a significant problem in docking validation, where accurate pose assessment determines whether a docking program is deemed successful or not.

Case Studies of Symmetry-Induced Artifacts

The limitations of conventional RMSD calculations manifest particularly in molecules with symmetric functional groups or whole-molecule symmetry. Ibuprofen, containing a symmetric aromatic ring, exemplifies molecules where naïve atomic correspondence produces misleading RMSD values [29]. Similarly, pyrrolidine-based HIV-1 protease inhibitors with C2-symmetry demonstrate how symmetric molecules can yield multiple chemically identical poses with different atomic correspondences [29] [40]. Without symmetry correction, docking programs may be unfairly penalized for generating correct poses that appear incorrect due to labeling discrepancies.

Table 1: Common Molecular Symmetry Types and RMSD Challenges

Symmetry Type	Example Molecules	RMSD Artifact	Biological Relevance
Aromatic rings	Benzene, ibuprofen	Rotation creates different atomic mappings	Ubiquitous in drug molecules
C2-symmetry	Pyrrolidine-based HIV-1 protease inhibitors	180° rotation creates alternative mappings	Common in synthetic enzyme inhibitors
Rotational symmetry	c-di-GMP	Multiple symmetric rotamers	Signaling molecules

Computational Solutions for Symmetry-Corrected RMSD

Algorithmic Approaches

Several computational strategies have been developed to address molecular symmetry in RMSD calculations:

• Closest-atom mapping (employed in AutoDock Vina): Maps each atom to the closest atom of the same element type. This approach can produce non-physical mappings where spatially close atoms are repeatedly matched while distant atoms remain unpaired [29].

• Hungarian algorithm (used in DOCK6): Frames atomic mapping as a cost-minimization assignment problem solved using combinatorial optimization. While more systematic than closest-atom mapping, this method ignores molecular connectivity and can generate mappings that break chemical bonds [29] [41].

• Graph isomorphism (implemented in DockRMSD and spyrmsd): Represents molecules as graphs with atoms as vertices and bonds as edges, then finds all possible isomorphic mappings that preserve the bonding network [29] [41]. This approach guarantees chemically meaningful atomic correspondences.

Tool Comparison and Selection Criteria

Table 2: Comparison of Symmetry-Corrected RMSD Tools

Tool	Algorithm	Implementation	Dependencies	Key Features
DockRMSD	Graph isomorphism with DEE pruning	C, with web server	Standalone	Deterministic minimal RMSD, handles complex symmetry
spyrmsd	Graph isomorphism	Pure Python	NumPy, SciPy	Easy Python integration, QCP superposition
OpenBabel obrms	VF2 graph isomorphism	C++ (within OpenBabel)	Full OpenBabel	Mature codebase, multiple file formats
DOCK6	Hungarian algorithm	Fortran/C++	DOCK6 package	Integrated with docking pipeline

DockRMSD: Protocol for Accurate Symmetry-Corrected RMSD Calculation

Theoretical Foundation: Graph Isomorphism with Dead-End Elimination

DockRMSD transforms symmetry correction into a graph isomorphism problem, where the optimal atomic mapping and RMSD calculation are performed through an exhaustive yet efficient search of all isomorphisms of the ligand structure graph [29] [40]. The algorithm consists of four key stages:

• Structure Input and Validation: Reads MOL2 format files for query and template ligand structures, verifying they represent the same molecule by comparing elements and bonding networks [29].

• Atom Identity Search: For each query atom, identifies all chemically equivalent template atoms by comparing element types and local bonding environments (including neighbor atoms and bond types) [29].

• Isomorphism Search with Feasibility Criteria: An exhaustive search applies three feasibility criteria: (1) one-to-one mapping restriction preventing template atom reuse, (2) bonding network consistency check ensuring mapped atoms maintain equivalent bonds, and (3) Dead-End Elimination (DEE) pruning paths that cannot yield lower RMSD than the current best [29].

• Optimal RMSD Calculation: Uses the identified optimal mapping to compute the final symmetry-corrected RMSD value [29].

Figure 1: DockRMSD Workflow for Symmetry-Corrected RMSD Calculation

Practical Implementation Protocol

Installation and Setup

Option 1: Native Compilation (Recommended for Performance)

Option 2: Web Server (No Installation) Access the online tool at https://aideepmed.com/DockRMSD/ for occasional use without local installation [42].

Option 3: Python Integration (via spyrmsd)

Input File Preparation

DockRMSD requires MOL2 format files with the following specifications:

• Complete atomic connectivity information
• Consistent element labeling
• Non-hydrogen atoms (unless hydrogen option specified)
• Structures pre-oriented based on receptor superposition [42]

Execution Command

Validation and Quality Control

To ensure accurate RMSD calculations:

• Verify bonding networks in input files using molecular visualization tools
• Confirm receptor superposition prior to ligand comparison
• Cross-validate with alternative tools (e.g., spyrmsd) for critical cases
• Inspect the mapping output for chemically reasonable atom assignments

Research Reagent Solutions

Table 3: Essential Tools for Symmetry-Corrected RMSD Analysis

Tool/Resource	Function	Application Context	Access
DockRMSD	Symmetry-corrected RMSD	Docking pose validation, symmetric ligands	Open-source [29]
spyrmsd	Python-based symmetry-corrected RMSD	Cheminformatics pipelines, ML workflows	Python Package Index [41]
OpenBabel obrms	Molecular file conversion + RMSD	Format conversion with symmetry correction	OpenBabel suite [29]
PyMOL	Molecular visualization	Result verification and visualization	Commercial with educational access
RDKit	Cheminformatics toolkit	Molecular graph representation	Open-source
MOL2 file format	Molecular structure representation	Standardized input for DockRMSD	Chemical table file format

Advanced Applications and Case Studies

Docking Benchmarking with Symmetric Molecules

In comprehensive docking benchmarks, DockRMSD revealed that traditional RMSD calculations overestimated pose errors for symmetric molecules by 30-50% compared to symmetry-corrected values [29]. This correction significantly impacts docking program evaluation, particularly for drug-like molecules frequently containing symmetric aromatic rings and functional groups.

spyrmsd Integration in Cheminformatics Pipelines

The pure Python implementation of spyrmsd enables seamless integration with modern cheminformatics and machine learning workflows [41]. Researchers can incorporate symmetry-corrected RMSD directly into automated pose analysis scripts, combining molecular graph representation with efficient isomorphism detection.

Limitations and Alternative Metrics

While symmetry correction addresses a fundamental RMSD limitation, researchers should consider complementary metrics for comprehensive pose evaluation:

• Template Modeling Score (TM-score): For global structure similarity
• Global Distance Test (GDT): For protein structure assessment
• Local Distance Difference Test (L-DDT): For local structure quality

Accurate RMSD calculation for symmetric molecules requires specialized tools that implement graph isomorphism algorithms to determine chemically relevant atomic mappings. DockRMSD and spyrmsd provide robust, open-source solutions that eliminate symmetry-induced artifacts in docking pose evaluation. By integrating these tools into structural bioinformatics workflows, researchers ensure fair and accurate assessment of computational docking performance, particularly for drug-like molecules with complex symmetry. The deterministic nature of graph isomorphism approaches guarantees identification of the minimal symmetry-corrected RMSD, establishing a reliable standard for pose comparison in computer-aided drug design.

Beyond the Basics: Troubleshooting Common RMSD Pitfalls and Limitations

The Root Mean Square Deviation (RMSD) is a fundamental metric in structural biology, providing a quantitative measure of the average distance between atoms of two superimposed protein structures. Its calculation involves optimal superposition of structures followed by computing the square root of the average squared distances between corresponding atoms [2]. While RMSD serves as a valuable global measure of structural similarity, it possesses a critical mathematical vulnerability: the squaring of distances in its calculation disproportionately amplifies the influence of large deviations [43]. This property makes RMSD highly sensitive to local structural variations in flexible regions, particularly loops and terminal domains, which can dominate the final value even when the core structural fold remains highly conserved.

This sensitivity presents a significant challenge known as the "outlier problem," where a small number of structurally divergent regions skew the global RMSD, potentially leading to misinterpretations about overall structural similarity and biological relevance. For researchers in drug discovery and protein engineering, this problem is particularly acute when comparing conformational states, analyzing molecular dynamics trajectories, or assessing structural predictions, as the biological function often depends on precise characterization of both stable cores and dynamic regions [21] [44].

Quantitative Impact of Structural Outliers

Magnitude of Skewing Effects

The impact of flexible loops and termini on global RMSD values is not merely theoretical but demonstrates measurable effects in practical applications. In benchmark studies comparing different conformational states of proteins, regions of high flexibility can contribute disproportionately to the final RMSD value.

Table 1: Comparative Performance of Structural Alignment Methods on ADK Conformations

Method	Final RMSD (Ã…)	Difference from Kabsch (Ã…)	Computational Time
Kabsch (Analytical)	7.130699	-	0.51 ms
Lie-RMSD (Adam)	7.130700	+0.000001	557.67 ms
Lie-RMSD (SGD)	7.130702	+0.000003	549.55 ms
Lie-RMSD (Sophia)	7.130710	+0.000011	587.31 ms
Lie-RMSD (AdamW)	7.130717	+0.000018	582.88 ms

Source: Benchmark data from Lie-RMSD study on Adenylate Kinase (4AKE vs 1AKE) [21]

The table demonstrates that while gradient-based optimization methods can achieve precision effectively identical to the analytical Kabsch algorithm, the reported RMSD values in the range of 7.13Ã… for the allosteric transition of Adenylate Kinase reflect significant conformational changes where flexible domains contribute substantially to the global measurement.

Biological Significance of Flexible Regions

The structural flexibility that complicates RMSD interpretation is often biologically essential. Complementarity-determining regions (CDRs) in antibodies and T-cell receptors exemplify this paradox—their conformational flexibility influences binding affinity and specificity, making them key to function while presenting challenges for structural comparison [44]. Similarly, intrinsically disordered proteins (IDPs) and regions, comprising approximately 30-40% of the human proteome, play crucial roles in cellular signaling and regulation but fundamentally resist characterization by RMSD-based metrics [45].

Complementary Metrics to Address RMSD Limitations

Advanced Structural Similarity Measures

To address the limitations of RMSD, several alternative metrics have been developed that provide more robust assessments of structural similarity.

Table 2: Protein Structural Comparison Metrics Beyond RMSD

Metric	Description	Advantages over RMSD	Typical Applications
GDT-HA (Global Distance Test-High Accuracy)	Measures the average percentage of Cα atoms under specified distance cutoffs (0.5, 1, 2, 4Å) after multiple superpositions	Less sensitive to local outliers; better reflects global fold conservation	CASP assessments; high-accuracy model evaluation [43]
SphereGrinder (SpG)	Computes local RMSD within 6Å spheres around each Cα atom; reports percentage under 2Å and 4Å cutoffs	Provides local quality assessment; identifies regions of structural variation	Local structure quality validation [43]
LDDT (Local Distance Difference Test)	Evaluates distance differences of atom-atom contacts without superposition	Rotation/translation invariant; captures local accuracy	AlphaFold confidence metric (pLDDT); model quality assessment [43]
TM-Score	Structure similarity measure based on length-dependent scale	Fair comparison of proteins of different lengths; more sensitive to global fold	General structure comparison [46]
MolProbity	Evaluates stereochemical quality (clashscores, rotamer, Ramachandran outliers)	Assesses physical plausibility rather than similarity to reference	Structure validation and refinement [43]

Integration of Flexibility Metrics

Recent approaches directly incorporate protein flexibility into structural assessment. The PEGASUS method predicts molecular dynamics-derived flexibility metrics, including root mean square fluctuation (RMSF), dihedral angle standard deviations, and average Local Distance Difference Test from sequence alone, achieving Pearson correlations of 0.75±0.02 for RMSF prediction on benchmark datasets [47]. Similarly, ITsFlexible classifies antibody and TCR CDR loops as "rigid" or "flexible" using graph neural networks, demonstrating that accounting for expected flexibility improves functional interpretation [44].

Experimental Protocols for Robust Structural Comparison

Protocol 1: Comprehensive Structural Assessment Pipeline

Title: Structural assessment workflow

Step 1: Structure Preparation

• Remove water molecules, ions, and cofactors unless specifically relevant to analysis
• Ensure identical atom selection between compared structures
• Address missing residues through either exclusion or modeling (document approach)
• For MD trajectory analysis, extract frames at consistent time intervals

Step 2: Core Structure Identification

• Perform initial global alignment using Kabsch algorithm or Lie-RMSD [21]
• Visually identify and exclude termini (typically 5-10 residues from N/C-termini)
• Identify flexible loops using B-factor analysis or prediction tools like PEGASUS [47]
• Define core structural elements comprising the stable protein fold

Step 3: Multi-Metric Analysis

• Calculate global all-atom RMSD for reference
• Compute core-only RMSD using identified stable regions
• Calculate GDT-HA or TM-score for global fold assessment [43] [46]
• Generate local quality measures (LDDT, SphereGrinder) for regional analysis [43]

Step 4: Flexibility Assessment

• Predict flexibility using sequence-based tools (PEGASUS) or experimental B-factors [47]
• For antibodies/TCRs, implement ITsFlexible for CDR flexibility classification [44]
• Correlate flexible regions with functional domains and biological significance

Step 5: Integrated Interpretation

• Contextualize global RMSD with core-only RMSD and GDT-HA
• Identify specific regions contributing to structural differences
• Relocate structural variations to biological function and evolutionary relationships

Protocol 2: Ensemble-Based Conformational Analysis Using FiveFold

For proteins with inherent flexibility or intrinsic disorder, single-structure comparison fails to capture conformational diversity. The FiveFold methodology addresses this through ensemble generation [45].

Title: FiveFold ensemble generation

Step 1: Multi-Algorithm Structure Generation

• Generate structural predictions using five complementary algorithms:
  • AlphaFold2: MSA-dependent, accurate for well-folded domains [45]
  • RoseTTAFold: MSA-dependent, strong long-range contact prediction [45]
  • ESMFold: MSA-independent, based on protein language models [45]
  • OmegaFold: MSA-independent, efficient for orphan sequences [45]
  • EMBER3D: MSA-independent, complementary approach [45]

Step 2: Protein Folding Shape Code (PFSC) Encoding

• Convert each predicted structure to PFSC representation
• Assign secondary structure states (H: α-helix, E: β-strand, B: β-bridge, G: 3₁₀-helix, I: Ï€-helix, T: turn, S: bend, C: coil) [45]
• Create standardized structural representations for comparison

Step 3: Protein Folding Variation Matrix (PFVM) Construction

• Analyze 5-residue windows across all five algorithm outputs
• Calculate frequency of each secondary structure state at each position
• Construct probability matrices for conformational states [45]

Step 4: Conformational Ensemble Generation

• Apply user-defined diversity criteria (minimum RMSD between conformations)
• Use probabilistic sampling from PFVM to select representative conformations
• Convert PFSC strings to 3D coordinates using homology modeling
• Apply stereochemical validation and quality filters [45]

Step 5: Ensemble-based Structural Comparison

• Calculate pairwise RMSD between all ensemble members
• Identify conserved core regions and flexible domains across ensemble
• Compute ensemble-averaged RMSD values for quantitative comparison
• Correlate conformational diversity with biological function

Research Reagent Solutions

Table 3: Essential Tools for Advanced Protein Structure Analysis

Tool Name	Type	Primary Function	Application Context
Lie-RMSD	Differentiable framework	Gradient-based structural alignment using Lie algebra	Flexible alternative to Kabsch; enables custom loss functions [21]
PEGASUS	Deep learning predictor	Sequence-based prediction of MD-derived flexibility metrics	Predicting RMSF, dihedral fluctuations from sequence [47]
ITsFlexible	Graph neural network classifier	Binary classification of CDR loops as rigid/flexible	Antibody/TCR engineering; flexibility assessment [44]
FiveFold	Ensemble method	Consensus conformational generation from 5 algorithms	IDP analysis; conformational diversity studies [45]
SARST2	Structural alignment algorithm	Rapid structural database search with filter-refine strategy	Large-scale structural comparison; database mining [16]
Rprot-Vec	Deep learning model	Sequence-based structural similarity prediction (TM-score)	Homology detection; function inference [46]
TM-align	Structural alignment	Protein structure comparison using TM-score	General structural similarity assessment [46]

The outlier problem presented by flexible loops and termini in RMSD calculation represents both a challenge and an opportunity in structural biology. By understanding the mathematical underpinnings of this limitation and implementing the multi-metric frameworks and experimental protocols outlined herein, researchers can transform a fundamental methodological vulnerability into a nuanced understanding of protein structure-function relationships. The integration of ensemble methods, machine learning flexibility prediction, and complementary similarity metrics enables a more comprehensive analysis that respects both the stable structural core and the dynamic regions essential for biological function. As structural biology continues to evolve toward modeling conformational landscapes rather than single static structures, these approaches will prove increasingly vital for drug discovery, protein engineering, and understanding the dynamic nature of the proteome.

The Root Mean Square Deviation (RMSD) is a fundamental metric in structural biology, used to quantify the average distance between the atoms of two superimposed protein structures [17]. It is most commonly calculated after the optimal rigid-body superposition of structures, typically using backbone atoms or Cα atoms [17] [3]. The standard equation for RMSD calculation is:

RMSD = √[ (1/N) × Σ(δ_i)² ]

where N represents the number of atom pairs, and δ_i is the distance between the i-th pair of equivalent atoms after superposition [17]. The value is expressed in length units, most commonly Ångströms (Å), where 1 Å equals 10⁻¹⁰ meter [17].

Despite its widespread use in fields such as protein structure prediction validation (e.g., in CASP experiments), molecular dynamics simulation analysis, and structural comparison for evolutionary studies, the RMSD metric possesses a significant limitation: its value is inherently dependent on the number of atoms (N) used in the calculation [5] [3]. This dependency creates a fundamental challenge when comparing structural similarities across proteins of different lengths, as a given RMSD value carries different implications for small versus large proteins [5]. This application note examines the source of this size dependency and provides detailed protocols for normalization approaches that enable more meaningful structural comparisons.

The Fundamental Problem: Why RMSD Depends on Protein Length

Mathematical and Statistical Foundations of Size Dependency

The dependency of RMSD on protein length stems from its mathematical formulation as a non-normalized average. In the RMSD equation, the summation occurs over all N atom pairs, meaning that structures with more atoms (longer proteins) inherently have more terms contributing to the sum [5]. Consequently, when comparing protein pairs of different sizes, the same numerical RMSD value does not indicate the same degree of structural similarity.

Statistical analysis reveals that the expected RMSD value increases with protein length even when comparing random structural arrangements. In a large-scale randomization experiment involving 72 million structural alignments of non-homologous proteins, researchers observed distinct RMSD distributions for proteins of different lengths [5]. This demonstrates that the RMSD's length dependency is not merely theoretical but empirically observable, fundamentally limiting its utility for cross-protein comparisons without normalization.

Practical Implications for Structural Biology Research

This size dependency has significant implications for structural biology research:

• Misleading Comparisons: An RMSD of 3Ã… has different structural implications for a 50-residue protein versus a 500-residue protein [5]. Without normalization, researchers might incorrectly conclude similar structural similarity for these disparate cases.
• Fold Assessment Challenges: In protein fold classification and structural evolution studies, quantitative comparison of RMSD values across different protein families becomes problematic [5].
• Prediction Validation Issues: In CASP and other structure prediction assessments, comparing model accuracy across targets of different lengths requires careful interpretation of raw RMSD values [3].

Table 1: Illustrative RMSD Values and Their Interpretation for Different Protein Sizes

Protein Size (Residues)	RMSD Value (Ã…)	Typical Structural Interpretation	Considerations for Length Dependency
50-100	1.0-2.0	Very high similarity	Comparable to experimental uncertainty; indicates essentially identical structures
50-100	3.0-4.0	Potentially significant differences	May indicate meaningful structural changes for small proteins
300-500	3.0-4.0	High similarity for core regions	For large proteins, may reflect only local flexibility or terminal region differences
300-500	6.0-8.0	Substantial structural differences	Likely indicates global fold differences or major conformational changes

Quantitative Evidence of RMSD Size Dependency

Experimental Demonstration Through Randomization Studies

Comprehensive evidence of RMSD's length dependency comes from a massive randomization study using 180 non-homologous protein structures selected from the Protein Data Bank [5]. The experimental methodology was as follows:

• Protein Selection: 180 non-homologous structures (maximum 25% sequence identity) representing diverse amino acid content, sequence length, and secondary structure composition [5].
• Randomization Protocol: Each native structure was compared with 400,000 randomized variants created through random shuffling of Cα equivalencies [5].
• Superposition and Calculation: All Cα atoms were included in superposing each native structure with all its variants using the Kabsch algorithm [5].
• Data Collection: The research team collected 72 million structural alignments (180 proteins × 400,000 variants) - an unprecedented dataset for analyzing RMSD behavior [5].

The results demonstrated unequivocally that RMSD distributions depend on protein size, with different characteristic RMSD limits observed for proteins of different lengths [5]. This systematic analysis provides the quantitative foundation for understanding why normalization is essential for meaningful structural comparisons across different protein families.

Comparative Analysis of Alternative Structural Measures

Recognition of RMSD's limitations has spurred the development of alternative metrics that are less dependent on protein size:

Table 2: Alternative Structure Comparison Metrics and Their Properties

Metric	Calculation Method	Size Dependency	Advantages	Common Applications
TM-score	Template Modeling score; length-dependent scale	Minimal	Provides probabilistic interpretation (0-1 range); >0.5 indicates same fold	Fold recognition, model quality assessment [48]
GDT (Global Distance Test)	Percentage of residues under specified distance cutoffs	Minimal	More robust to outlier regions; expressed as percentage	CASP assessments; model quality evaluation [17]
nRMSD (Normalized RMSD)	RMSD divided by normalization factor based on protein length	Corrected	Enables direct comparison across different protein sizes	Evolutionary studies; fold classification [5]
wRMSD (Weighted RMSD)	Gaussian-weighted RMSD fit; reduced weight for mobile regions	Reduced	Identifies structurally invariant core; handles flexibility better	Comparing flexible proteins; conformational change analysis [22]

Protocols for RMSD Normalization and Size-Independent Comparison

Normalized RMSD (nRMSD) Calculation Protocol

Based on the research by Carugo and Pongor, the following protocol produces a normalized RMSD that enables comparison across proteins of different sizes [5]:

Experimental Principle: nRMSD adjusts the traditional RMSD using a normalization factor derived from the distribution of RMSD values obtained by comparing the protein against a large number of its randomized structural variants [5].

nRMSD Calculation Workflow

Materials and Reagents:

• Native protein structure (PDB format)
• Computational resources for large-scale structural randomization and comparison
• Kabsch superposition algorithm implementation [5]
• Statistical analysis software (R, Python, or similar)

Step-by-Step Procedure:

• Input Native Structure: Obtain the three-dimensional coordinates of the native protein structure in PDB format.
• Generate Randomized Variants: Create 400,000 randomized structural variants through random shuffling of Cα equivalencies while maintaining the protein's covalent geometry [5].
• Perform Structural Superpositions: For each randomized variant, perform optimal superposition with the native structure using the Kabsch algorithm applied to all Cα atoms [5].
• Calculate RMSD Distribution: Compute the RMSD between the native structure and each randomized variant, building a comprehensive distribution of RMSD values.
• Establish Length-Specific RMSD Profile: Characterize the distribution with appropriate statistical parameters (mean, percentiles) that define the expected RMSD behavior for proteins of this size.
• Normalize Query RMSD: When comparing two actual protein structures, calculate their traditional RMSD, then normalize it using the established length-specific profile to obtain nRMSD [5].

Technical Notes:

• This method requires substantial computational resources for the initial randomization studies.
• The normalization factor is protein-specific, accounting for individual structural properties beyond just length.
• Pre-computed normalization factors for common protein folds can accelerate future analyses.

Practical Protocol for Size-Independent Structural Comparison

For researchers requiring practical, computationally feasible approaches for size-independent structural comparison, the following integrated protocol is recommended:

Experimental Principle: This protocol combines multiple size-independent metrics to provide a comprehensive assessment of structural similarity, leveraging TM-score and local RMSD analysis to complement global RMSD measurements [3] [48].

Materials and Reagents:

• Two protein structures to compare (PDB format)
• Structure comparison software with TM-score capability (TM-align, PyMOL plugins)
• Local alignment algorithms (LGA, DALI, or CE for optional local similarity analysis)
• Visualization tools (PyMOL, Chimera) for structural interpretation

Step-by-Step Procedure:

• Global RMSD Calculation:
  • Superimpose structures using Kabsch algorithm to minimize global RMSD
  • Calculate Cα RMSD using standard equation
  • Record RMSD value and number of residues compared

• TM-score Calculation:

  • Calculate TM-score using TM-align or equivalent software
  • Interpret results: TM-score >0.5 indicates same fold; TM-score <0.17 indicates random similarity
  • Note that TM-score is length-scaled by default, enabling cross-protein comparison

• Local Similarity Analysis:

  • Identify largest contiguous substructure with RMSD below 2.0Ã…
  • Calculate Local Distance Difference Test (LDDT) for binding sites or functional regions
  • Use iterative superposition methods to identify structurally invariant core

• Weighted RMSD for Flexible Proteins:

  • For proteins with flexible regions, apply Gaussian-weighted RMSD (wRMSD)
  • wRMSD assigns lower weights to mobile regions, focusing superposition on structurally conserved core [22]
  • Use iterative re-weighting until convergence to identify optimal superposition

Interpretation Guidelines:

• For proteins of different sizes: Prioritize TM-score (threshold >0.5) over raw RMSD for fold-level comparisons
• For similar-length proteins: RMSD <2.0Ã… indicates high similarity; RMSD >4.0Ã… indicates substantial differences
• For flexible proteins: Focus on wRMSD and local similarity measures rather than global RMSD
• Always consider biological context: Functional regions may require specific analysis regardless of global measures

The Scientist's Toolkit: Essential Research Reagents and Computational Solutions

Table 3: Key Research Reagents and Computational Tools for RMSD Analysis and Normalization

Tool/Resource	Type	Primary Function	Implementation Considerations
Kabsch Algorithm	Algorithm	Optimal superposition for RMSD minimization	Foundation for most RMSD calculations; implemented in many packages [17]
GROMACS gmx rms	Software Module	RMSD calculation from MD trajectories	Integrates with molecular dynamics workflows; supports time-series analysis [49]
TM-align	Standalone Program	TM-score calculation and structure alignment	Provides size-independent structural comparison; useful for fold assessment [48]
SARST2	Structural Alignment Algorithm	High-throughput structural database searching	Uses filter-and-refine strategy; efficient for massive database searches [16]
wRMSD Implementation	Algorithmic Approach	Gaussian-weighted RMSD superposition	Handles flexible proteins; reduces influence of mobile regions [22]
LGA (Local-Global Alignment)	Alignment Algorithm	Sequence-independent structure alignment	Identifies local similarities despite global differences [3]

The dependency of RMSD on protein length presents a fundamental challenge in structural biology that requires normalization strategies for meaningful cross-protein comparisons. The protocols outlined herein—particularly the normalized RMSD approach and the integration of TM-score—provide researchers with practical methodologies to overcome this limitation. As structural biology enters an era of exponentially increasing data, with resources like the AlphaFold Database containing over 214 million predicted structures [16] [50], the importance of robust, size-independent comparison metrics will only grow. Future developments will likely involve more sophisticated probabilistic superposition methods [51] and machine learning-enhanced alignment algorithms [16] that automatically account for length dependencies while providing biologically interpretable similarity measures. By adopting these normalized approaches, researchers can ensure their structural comparisons yield biologically meaningful insights regardless of the proteins' sizes.

Protein structure comparison is a fundamental task in structural bioinformatics, with the Root Mean Square Deviation (RMSD) of atomic positions serving as the traditional metric for quantifying structural differences. Global RMSD, calculated after rigid-body superposition, provides a single average value for the entire structure but is dominated by the most variable regions, often obscuring conserved, functionally critical cores. This application note details the limitations of global RMSD and presents advanced, localized alignment strategies—including flexible superposition, core-focused scoring, and chemical-environment comparison—that provide a more nuanced, biologically relevant understanding of protein structural relationships. We provide explicit protocols for implementing these methods using widely available tools, empowering researchers to extract deeper insights from structural data for applications in evolutionary analysis, function prediction, and drug development.

The Limitations of Global RMSD

The Root Mean Square Deviation (RMSD) measures the average distance between atoms—typically backbone Cα atoms—of two superimposed protein structures [17]. It is mathematically defined for two sets of n equivalent atom vectors, v and w, as: [ \mathrm{RMSD} (\mathbf{v}, \mathbf{w}) = \sqrt{\frac{1}{n}\sum{i=1}^{n}\|vi - w_i\|^2} ] Despite its widespread use, global RMSD has significant drawbacks [3]:

• Sensitivity to Outliers: The RMSD value is dominated by the largest errors because the deviations are squared before averaging. A small number of highly displaced regions, such as flexible loops or termini, can disproportionately inflate the RMSD, making two globally similar structures appear dissimilar.
• Dependence on Alignment Length: RMSD values are directly dependent on the number of equivalent residues (EQR) in the alignment, making it difficult to compare similarity scores across protein pairs of different lengths [52].
• Rigid-Body Assumption: Standard RMSD calculation relies on an optimal rigid-body superposition, an approach that fails for proteins involving conformational changes, domain movements, or inherent flexibility [3] [10]. For instance, global backbone RMSD struggles to distinguish between a pair of structures with a single displaced helix and another pair with multiple small-scale rearrangements [3].

Advanced Metrics for Structural Comparison

To overcome the limitations of global RMSD, several sophisticated metrics and methods have been developed. These can be broadly categorized into distance-based, score-based, and local environment-focused measures.

Table 1: Advanced Metrics for Protein Structure Comparison

Metric	Type	Description	Key Features & Advantages
TM-score [10] [53]	Score-based	Measures topological similarity using a length-independent scoring function.	- Ranges from 0-1; >0.5 indicates same fold, <0.2 indicates random similarity.- Less sensitive to local errors than RMSD.- Unified scoring function allows comparison across molecular types.
Gaussian-weighted RMSD (wRMSD) [22]	Distance-based	Overlay using a Kabsch-based least-squares method where atoms are weighted by their displacement.	- Weights atoms inversely to their movement; stable regions have greater influence.- Highlights flexibility ranges in overlaid structures.- Useful for comparing conformations of the same protein.
Local Distance Difference Test (lDDT) [54]	Local environment	Evaluates local consistency by comparing distance differences between atoms within a defined cutoff.	- Superimposition-independent.- Robust against local errors and structural outliers.- Assesses the quality of local geometry.
Local Composition Hellinger Distance (LoCoHD) [54]	Local environment	Measures chemical and structural differences between local residue environments based on primitive atom types.	- Focuses on chemical composition of local environments, not just backbone geometry.- Can distinguish between residues with different physicochemical properties.- Provides unique information complementary to RMSD and lDDT.

Protocols for Local and Core-Focused Alignments

Protocol 1: Flexible Alignment with FATCAT

Objective: To compare protein structures that may have undergone conformational changes using a flexible alignment algorithm.

Background: The FATCAT (Flexible structure AlignmenT by Chaining Aligned fragment pairs allowing Twists) algorithm accommodates relative mobility between domains or subdomains by introducing "twists" (hinges) between independently aligned, rigid parts [10]. This is crucial for comparing different conformational states (e.g., apo and holo forms) or proteins with distant evolutionary relationships.

Materials:

• Input: 3D coordinate files for two protein structures (in PDB, mmCIF, or bcif format).
• Software: US-align command-line tool or RCSB PDB Pairwise Structure Alignment web server [10] [53].

Procedure:

• Access the Tool: Navigate to the RCSB PDB Structure Alignment tool or download and install US-align.
• Input Structures: Specify the reference and target structures using PDB IDs, UniProt IDs, or by uploading coordinate files.
• Select Algorithm: Choose the jFATCAT-flexible algorithm from the available methods.
• Execute Alignment: Run the alignment. The algorithm will automatically identify potential hinge points and align rigid blocks.
• Interpret Results:
  • RMSD: Examine the reported RMSD, remembering it is calculated only on aligned residues.
  • TM-score: Note the TM-score to evaluate overall topological similarity.
  • Alignment Visualization: Use the integrated Mol* viewer or PyMOL to visually inspect the superposition, paying attention to how different domains are aligned and the location of introduced twists.

Protocol 2: Core Alignment Using Iterative Superposition

Objective: To identify and align the structurally conserved core, minimizing the influence of variable regions.

Background: This protocol uses an iterative process to find the largest superimposable core. It is inspired by algorithms that optimize superimposition by assigning lower weights to deviating fragments, thereby finding the largest common core [3].

Materials:

• Input: 3D coordinate files for two protein structures.
• Software: US-align command-line tool or any structural alignment tool that provides a core-focused alignment (e.g., methods using TM-score optimization) [53].

Procedure:

• Initial Alignment: Perform an initial sequence-independent global alignment using US-align or a similar tool.
• Identify Poorly Aligned Regions: Analyze the initial alignment and identify residues with high Cα atomic distances (e.g., >3.8 Ã…).
• Iterative Refinement: The algorithm iteratively re-optimizes the superposition by focusing on the best-aligned residues, effectively down-weighting or excluding outliers.
• Core Definition: The final alignment represents the core. The number of equivalent residues in this core and their associated RMSD (Core-RMSD) are key outputs.
• Analysis: Compare the Core-RMSD to the global RMSD from a rigid-body alignment. A significantly lower Core-RMSD indicates the presence of a well-conserved structural core despite peripheral variations.

Protocol 3: Assessing Local Chemical Environments with LoCoHD

Objective: To compare protein structures based on the chemical composition of local residue environments, going beyond backbone geometry.

Background: The LoCoHD (Local Composition Hellinger Distance) metric quantifies the dissimilarity between two local environments in proteins based on the distribution of primitive atom types (e.g., aromatic carbon, charged nitrogen) within a defined radius [54]. This captures changes in chemical interaction networks (e.g., salt bridges, hydrophobic contacts).

Materials:

• Input: 3D coordinate files for two protein structures to be compared.
• Software: LoCoHD implementation (source code or standalone tool).

Procedure:

• Define Primitive Typing Scheme: Choose a set of chemical primitive types (e.g., FA+Cent which includes residue centroids) for the analysis.
• Set Weight Function: Define the distance weighting function (e.g., uniform weighting between 3 Ã… and 10 Ã…).
• Calculate Pairwise Scores: For each residue in one structure, compute the LoCoHD score against one or more residues in the other structure. A score of 0% indicates identical environments, while higher scores indicate greater chemical dissimilarity.
• Interpret Results:
  • Global Analysis: Map per-residue LoCoHD scores onto the 3D structure to identify regions of high chemical conservation or variation.
  • Statistical Context: Compare scores to known distributions; for example, a score above ~40% is considered large for random residue-pairs using the FA+Cent scheme [54].
  • Biological Insight: Use the results to infer functional implications, such as conserved active sites or altered binding interfaces.

The Scientist's Toolkit: Research Reagent Solutions

Table 2: Essential Resources for Protein Structure Comparison

Resource / Tool	Type	Primary Function	Access
US-align [53]	Software	Universal structure alignment for proteins, nucleic acids, and complexes using TM-score.	Command line, Web server
RCSB PDB Pairwise Alignment [10]	Web Server	User-friendly interface for multiple algorithms (jFATCAT, CE, TM-align).	Web browser
DEDAL [55]	Software & Web Server	Non-sequential, non-rigid-body alignment using local descriptors; handles difficult similarities.	Web server
LoCoHD [54]	Software / Metric	Quantifies chemical environment dissimilarity between local regions in structures.	Source code
VAST+ [56]	Web Tool / Database	NCBI's tool for finding and aligning structurally similar neighbors from the MMDB.	Web browser

The reliance on global RMSD as a sole measure of protein structural similarity is a limitation that can obscure critical biological insights. The advanced methods and protocols outlined here—flexible alignment with FATCAT, core-finding iterative superposition, and local chemical environment analysis with LoCoHD—provide a powerful, multi-faceted toolkit for researchers. By moving beyond a single, global average to examine local structural cores and chemical landscapes, scientists can achieve a more accurate and profound understanding of structure-function relationships, evolutionary dynamics, and the structural basis of disease, thereby accelerating discovery in structural biology and rational drug design.

The root mean square deviation (RMSD) is a foundational metric for quantifying the structural similarity between two protein structures by measuring the average distance between corresponding atoms after optimal superposition [57]. Despite its widespread use, the global RMSD has a significant drawback: it is dominated by the largest errors within the structure [3]. This makes it poorly representative of the overall degree of structural similarity when proteins undergo conformational changes, a common biological phenomenon. Proteins are not static entities; they exhibit internal movements ranging from side-chain rotations to large-scale domain or subdomain displacements [58]. When using rigid-body alignment methods, which treat proteins as unchanging objects, these movements can prevent the correct identification of structurally equivalent regions, especially when the conformational change is large [58] [3].

The necessity for flexible alignment becomes evident in cases like the molecular chaperone GroEL or active and inactive conformations of receptors such as estrogen receptor α (ERα). For example, the transition between active and inactive states of ERα involves the movement of a single helix (Helix 12). A rigid-body alignment of these two states would result in a high global RMSD, obscuring the fact that the majority of the structure remains largely unchanged [3]. Similarly, in GroEL, the polypeptide chain folds back onto itself, creating structural domains from sequence-distant segments. Rigid aligners struggle to recognize these spatially continuous but sequence-discontinuous domains [58]. Therefore, while rigid-body alignment and RMSD are suitable for comparing very similar, static structures, they fail to provide a biologically meaningful comparison for flexible proteins.

Flexible Alignment Algorithms: Core Concepts and Methods

Flexible alignment algorithms overcome the limitations of rigid-body assumptions by allowing for internal movements within the protein structures during comparison. The core principle involves treating a protein not as a single rigid body, but as an assembly of multiple rigid bodies connected by flexible hinges [58]. The goal is to find an optimal equivalence map between the residues of two structures while simultaneously identifying the locations of these hinges.

Key Concepts and Terminology

• Matching Fragment Pairs (MFPs): These are short, ungapped stretches of residues from two structures that are structurally similar. They serve as the basic building blocks from which a flexible alignment is constructed [58].
• Structurally Conserved Regions (SCRs): These are sets of aligned residues for which the distances between Cα atoms are identical within a defined tolerance across different conformations. SCRs can be continuous in space but discontinuous in the amino acid sequence [58].
• Hinge Regions: The flexible regions, often loops or linker domains, that connect rigid blocks and about which domain movements occur.

Several computational strategies have been developed to perform flexible structural alignment. RAPIDO (Rapid Alignment of Proteins in terms of Domains) is one such algorithm designed to align protein structures in the presence of large conformational changes [58]. Its algorithm consists of four main steps:

• Search for MFPs: An exhaustive search identifies short, structurally similar fragments between the two structures.
• Chaining of MFPs: A graph-based algorithm connects compatible MFPs into a preliminary alignment.
• Refinement: The initial alignment is refined to improve accuracy.
• Identification of Rigid Bodies: A genetic algorithm is applied to identify the structurally conserved regions (SCRs) based on analysis of difference distance matrices [58].

An alternative approach is found in methods based on elastic shape analysis. This mathematical framework treats protein backbones as continuous three-dimensional curves. The alignment problem is transformed into comparing the shapes of these curves, which can bend and stretch to accommodate conformational changes and insertions/deletions. A formal distance, the geodesic distance, is computed as a measure of dissimilarity, providing a proper metric for statistical analysis [59].

Other notable tools in this category include FATCAT (Flexible structure AlignmentT by Chaining Aligned fragment pairs allowing Twists), which introduces twists around pivots in the alignment, and FlexProt [58].

Quantitative Comparison of Alignment Methods

The performance and characteristics of rigid-body and flexible alignment methods can be quantitatively compared across several key metrics. The following tables summarize these differences and provide performance data from method evaluations.

Table 1: Characteristics of Protein Structure Comparison Methods

Feature	Rigid-Body Aligners (e.g., CE, DALI, TM-align)	Flexible Aligners (e.g., RAPIDO, FATCAT)
Core Assumption	Protein structures are treated as single, unchanging objects.	Proteins comprise rigid blocks connected by flexible hinges.
Handling Flexibility	Poor; performance degrades with increasing conformational change.	Explicitly models flexibility, allowing for internal movements.
Typical Output	A single rotation/translation matrix and a global RMSD value.	An alignment, a set of rigid bodies (SCRs), and hinge locations.
Best Application	Comparing highly similar structures (e.g., mutant variants).	Comparing conformers (e.g., apo/holo forms, different functional states).
Sequence Continuity	Typically produces alignments continuous in sequence.	Can identify SCRs that are continuous in space but not in sequence.

Table 2: Performance Comparison on Kinase Structures and GPCR Dock 2010 Models

Method Type	Example Algorithm	Performance on Kinases	Performance on GPCR Dock Models (Backbone RMSD)	Sensitivity in Detecting Similarities
Rigid-Body	Conventional RMSD minimization	Fails to align domains undergoing large movements [58].	~2.3 Ã… for easier homology modeling case [3].	Misses similarities obscured by domain motions [58].
Flexible	RAPIDO	Capable of detecting similarities missed by rigid aligners [58].	More accurate for targets with conformational changes [60].	Higher; reliably detects discontinuous SCRs [58].
Flexible	FATCAT	Allows for limited flexibility through twists [58].	Not specifically reported in search results.	Moderate [58].

Experimental Protocol: Performing a Flexible Structure Alignment with RAPIDO

This protocol details the steps for comparing two protein structures with large conformational changes using the RAPIDO algorithm, from data preparation to interpretation of results.

Research Reagent Solutions

Table 3: Essential Materials and Software for Flexible Alignment

Item Name	Function/Description	Example/Format
Protein Structures	The input data for comparison. Typically obtained from the Protein Data Bank (PDB).	PDB format files (.pdb).
RAPIDO Software	The executable program that performs the flexible alignment.	Downloadable from the official repository or bioinformatics toolkits.
Computing Environment	A standard computer workstation capable of running the software.	Linux, macOS, or Windows command line interface.
Visualization Software	Used to visualize and analyze the results, including superpositions and hinge regions.	PyMOL, UCSF Chimera, or VMD.

Step-by-Step Procedure

• Input Data Preparation

  • Obtain the three-dimensional atomic coordinates for the two protein structures to be compared in PDB format.
  • Ensure the files contain at least the Cα atoms for each residue. The algorithm uses Cα coordinates for the initial alignment [58].

• Running RAPIDO Alignment

  • Execute the RAPIDO program via the command line, specifying the two input PDB files as arguments.
  • Use the default parameters for a standard analysis, which are optimized to prioritize the geometric similarity (low RMSD) of structurally conserved regions over the sheer length of the alignment [58].
  • The algorithm will automatically proceed through its four-step pipeline: finding MFPs, chaining them, refining the alignment, and identifying rigid bodies.

• Analysis of Output Data

  • Structurally Conserved Regions (SCRs): Examine the output to identify the regions classified as SCRs. These are the conformationally invariant parts of the structure.
  • Superposition: Use the transformation matrices provided by RAPIDO for each SCR to superpose the two structures. This superposition will highlight the conserved core and the divergent, flexible regions.
  • Hinge Detection: The boundaries between consecutive rigid bodies indicate the location of hinge points or flexible linkers responsible for the observed conformational change.

• Interpretation and Validation

  • Biologically interpret the results by correlating the identified SCRs with functional domains (e.g., active sites, binding pockets).
  • Validate the alignment by checking if the RMSD within each individual SCR is low, confirming their conformational invariance.

Diagram 1: RAPIDO Flexible Alignment Workflow

Flexible alignment algorithms such as RAPIDO and those based on elastic shape analysis are essential tools for moving beyond the constraints of rigid-body assumptions. By explicitly accounting for protein flexibility, these methods enable a more accurate and biologically meaningful comparison of protein structures undergoing conformational changes. They allow researchers to dissect complex molecular movements into rigid-body rotations and translations connected by hinges, providing deeper insights into the dynamics underlying protein function. For any research involving the comparison of different conformational states, ligand-bound and unbound structures, or proteins with known domain movements, flexible alignment should be the method of choice over traditional rigid-body approaches.

Root Mean Square Deviation (RMSD) is a fundamental metric in structural biology, providing a quantitative measure of similarity between two superimposed sets of atomic coordinates. When comparing protein structures, researchers calculate RMSD to evaluate conformational changes, assess computational model quality against experimental structures, and analyze structural conservation across evolutionary relatives. The mathematical definition of RMSD involves the square root of the average squared distances between corresponding atoms in two superimposed structures: RMSD = √[ (1/n) × Σ(di)² ], where n represents the number of atom pairs and di is the distance between the i-th pair of equivalent atoms after optimal superposition [3].

Despite its widespread use, RMSD has significant limitations that researchers must acknowledge. The metric is dominated by regions with the largest deviations, meaning that a single poorly-aligned flexible region can disproportionately inflate the RMSD value even when the remaining structural core aligns well. Furthermore, RMSD values are highly sensitive to the number of atoms included in the calculation and the specific method used for structural alignment, creating challenges for comparing results across different studies [3] [26]. This application note establishes rigorous protocols for RMSD calculation and reporting to enhance reproducibility and accuracy in protein structure research.

Key Considerations for RMSD Calculation

Defining Atomic Correspondences

Before calculating RMSD, researchers must explicitly define which atoms will be included in the comparison and establish residue-residue correspondence between the structures. Sequence-dependent methods assume strict one-to-one correspondence between target and model residues based on their sequence order, while sequence-independent methods identify structural equivalences through algorithmic superposition, accommodating scenarios like circular permutations or incorrect sequence threading [3] [10].

For most protein structure comparisons, the recommended practice is to calculate RMSD using Cα atoms of the protein backbone, as these provide a consistent framework for assessing overall fold similarity. However, researchers studying specific functional regions might calculate RMSD for binding site residues or all heavy atoms in particular regions of interest. Whatever the approach, the selected atoms and correspondence method must be explicitly documented to ensure reproducibility [3] [10].

Superposition Methods

RMSD calculation requires optimal superposition of the structures being compared through rigid-body transformation. Different superposition algorithms can yield meaningfully different RMSD values, making methodological transparency essential. The jCE (Combinatorial Extension) algorithm identifies segments with similar local structure and combines them to maximize aligned residues while minimizing RMSD. Alternatively, jFATCAT-rigid performs rigid-body alignment to identify the largest structurally conserved core, while jFATCAT-flexible introduces hinges to accommodate conformational changes between domains. For global topology comparison, TM-align uses dynamic programming to generate sequence-independent alignments optimized for TM-score, which also provides RMSD as an output metric [10].

Table 1: Common Structural Alignment Algorithms and Their Applications

Algorithm	Alignment Type	Key Features	Best Use Cases
jCE	Rigid-body	Combines similar local segments; maximizes residues with low RMSD	Comparing structures with same topology and minimal conformational changes
jFATCAT-rigid	Rigid-body	Identifies largest structurally conserved core	General purpose comparison of homologous proteins
jFATCAT-flexible	Flexible	Introduces twists/hinges between rigid domains	Comparing structures with domain movements or conformational changes
jCE-CP	Flexible	Accommodates circular permutations	Comparing proteins with different loop connectivities or permuted domains
TM-align	Sequence-independent	Focuses on global topology; provides TM-score	Fold-level comparison, especially for distant homologs
Smith-Waterman 3D	Sequence-dependent	Uses sequence similarity with structural validation	Comparing close homologs with high sequence identity

Experimental Protocol for RMSD Calculation

Workflow for Structural Comparison

The following workflow diagram outlines the standardized protocol for protein structure comparison and RMSD calculation:

Step-by-Step Protocol

Step 1: Structure Preparation and Preprocessing

Begin by obtaining high-quality structural coordinates from the Protein Data Bank (PDB) or computational modeling outputs. For experimental structures, consult validation reports to identify poorly resolved regions. Remove crystallographic additives (e.g., glycerol, DMSO) unless they are relevant to the biological question. Select the appropriate biological assembly when dealing with multimeric proteins. For mutant studies or engineered proteins, ensure the wild-type and variant structures have comparable resolution and data quality [61].

Step 2: Define Comparison Scope and Biological Context

Explicitly document the scientific question driving the structural comparison. Are you assessing model accuracy, analyzing conformational changes, or evaluating structural conservation? Based on this objective, select the appropriate structural regions for comparison. For global fold assessment, include all structured regions with well-defined electron density. For functional site analysis, focus on residues comprising binding pockets or catalytic centers. Always report the specific residue ranges and atom types included in the analysis [61] [10].

Step 3: Select and Apply Alignment Algorithm

Choose an alignment algorithm appropriate for your biological question (refer to Table 1). For most applications, begin with jFATCAT-rigid or TM-align through the RCSB PDB Pairwise Structure Alignment tool. For structures with known conformational flexibility, consider jFATCAT-flexible. Execute the alignment using default parameters first, then document any parameter modifications. Most tools provide an option to output the transformation matrix used for superposition—retain this information for reproducibility [10].

Step 4: Calculate RMSD and Complementary Metrics

Calculate RMSD using the formula provided in Section 1. Most alignment tools automatically compute this value. Additionally, calculate at least one complementary metric such as TM-score (measures topological similarity on a 0-1 scale, where >0.5 indicates same fold) or GDT (Global Distance Test, measures percentage of residues within defined distance cutoffs). These metrics provide context for interpreting RMSD values, particularly when comparing structures of different sizes or when local deviations affect global RMSD [6] [10] [62].

Step 5: Validation and Quality Control

Implement validation checks to ensure robust results. Visually inspect the superposition using molecular visualization software (e.g., PyMOL, Mol*). Check for outliers that disproportionately influence RMSD. Run negative controls by comparing your structure to unrelated folds to establish baseline RMSD values. For computational models, compare against multiple experimental structures if available. Report the number of equivalent residues used in the RMSD calculation, as this significantly impacts interpretation [61] [10].

Reporting Standards and Data Interpretation

Essential Metadata for Reporting

Comprehensive reporting of RMSD analyses requires both quantitative results and methodological context. The following table outlines critical information that must accompany any reported RMSD value:

Table 2: Essential Elements for Reporting RMSD Analyses

Reporting Element	Description	Example
Structures Compared	PDB IDs or model identifiers with chain information	"4HHB chain A vs. 1OJ6 chain A"
Alignment Method	Algorithm and version used	"TM-align (20220415)"
Atoms Included	Type of atoms used in calculation	"Cα atoms"
Residue Range	Specific residues included in alignment	"Residues 15-242 (structured regions only)"
Number of Equivalent Residues	Count of residue pairs in final alignment	"185 residue pairs"
RMSD Value	Calculated RMSD in Ångströms	"2.3 Å"
Complementary Metrics	TM-score, GDT, or other relevant measures	"TM-score = 0.68"
Software & Version	Tools used for calculation	"RCSB PDB Pairwise Alignment tool v3.5"

Interpreting RMSD Values in Context

RMSD values require careful interpretation relative to the biological system and comparison type. For high-resolution model assessment against experimental structures, RMSD values below 1.0 Ã… typically indicate excellent agreement, while values between 1.0-2.0 Ã… represent good agreement. For comparative analysis of conformational changes in identical proteins, RMSD values of 0.5-3.0 Ã… often reflect biologically relevant transitions. When comparing homologous proteins with divergent sequences, RMSD values below 2.5 Ã… generally indicate high structural conservation, while values between 2.5-4.0 Ã… suggest moderate conservation with local variations [3] [10].

Crucially, always consider RMSD in conjunction with the number of aligned residues. A low RMSD based on a small subset of residues may be less biologically meaningful than a slightly higher RMSD encompassing the entire structured domain. Similarly, RMSD values from different studies should only be directly compared when the methodologies (alignment algorithm, atom selection, residue ranges) are equivalent.

Table 3: Essential Resources for Protein Structure Comparison

Resource	Type	Function	Access
RCSB PDB Pairwise Structure Alignment	Web Tool	Perform multiple alignment algorithms through standardized interface	https://www.rcsb.org/docs/tools/pairwise-structure-alignment
Mol*	Visualization Tool	Interactive visualization of superposed structures with measurement capabilities	Integrated in RCSB PDB or standalone
DALI	Web Server	Distance matrix-based alignment for remote homology detection	http://ekhidna2.biocenter.helsinki.fi/dali/
TM-align	Standalone Program	Sequence-independent alignment optimized for TM-score calculation	https://zhanggroup.org/TM-align/
PyMOL	Visualization Software	Molecular visualization with robust superposition and measurement tools	Commercial with educational license
CLESUM	Database	Substitution matrices for local substructure evolutionary relationships	Available through academic distribution
SIFTS	Database	Mapping between PDB, UniProt, and structural classification systems	https://www.ebi.ac.uk/pdbe/docs/sifts/

RMSD in Context: Validation and Comparison with Advanced Structural Metrics

The comparison of three-dimensional protein structures is a fundamental task in structural biology, crucial for understanding evolutionary relationships, inferring protein function, and guiding drug discovery efforts. For decades, the Root Mean Square Deviation (RMSD) has served as the predominant quantitative measure for assessing structural similarity between two sets of atomic coordinates. RMSD is defined as the square root of the average squared distance between corresponding atoms after optimal superposition, calculated as:

RMSD = √[ (1/n) × Σ(d_i)² ]

where n is the number of atom pairs and d_i is the distance between the i-th pair of equivalent atoms after superposition [1] [3]. The calculation requires solving for the optimal rotation and translation that minimizes this value, typically achieved through algorithms such as the Kabsch method [51].

Despite its widespread adoption, RMSD possesses inherent limitations that compromise its effectiveness as a standalone metric for structural comparison. As a global average dominated by the largest deviations, RMSD can mask significant local variations and is highly sensitive to outlier regions [3] [51]. This review examines the critical shortcomings of RMSD and introduces a suite of complementary metrics that provide a more nuanced, robust, and biologically relevant assessment of protein structural similarity.

Limitations of RMSD in Structural Analysis

Sensitivity to Outliers and Dominance by Large Deviations

As a least-squares measure, RMSD is disproportionately influenced by regions with the largest structural deviations. A single divergent loop or flexible terminus can substantially increase the RMSD value even when the core structural elements align well [3] [51]. This sensitivity to outliers makes RMSD poorly suited for comparing structures that undergo domain movements or local conformational changes, as it may overestimate overall structural differences.

Dependence on Superposition and Atom Selection

RMSD values are highly dependent on both the quality of structural superposition and the selection of atoms included in the calculation. Optimal superposition that minimizes RMSD may not always represent the biologically most relevant alignment, particularly for multi-domain proteins or structures with substantial flexible regions [3]. Furthermore, the choice of atom subsets (e.g., Cα atoms only versus all backbone atoms) can yield significantly different RMSD values, complicating cross-study comparisons.

Poor Correlation with Biological Relevance

Perhaps the most significant limitation of RMSD is its weak correlation with biological function. Structures with low RMSD may exhibit crucial functional differences at binding sites, while proteins with higher RMSD might share functionally equivalent active sites [3]. This disconnect arises because RMSD measures purely geometric similarity without considering the structural context or functional constraints.

Table 1: Key Limitations of RMSD in Protein Structure Comparison

Limitation	Description	Impact on Assessment
Outlier Sensitivity	Dominated by regions with largest deviations	Overestimates global structural differences; masks local similarities
Size Dependency	Value scales with number of residues compared	Difficult to compare values across different protein sizes or domains
Superposition Dependence	Optimal RMSD superposition may not be biologically relevant	May produce misleading alignments of functional regions
Lack of Normalization	No inherent scale (0 to ∞)	No intuitive meaning; difficult to interpret in isolation
Insensitivity to Local Quality	Global average obscures local variations	Poor indicator of binding site preservation or local structural integrity

Complementary Metrics for Protein Structure Comparison

To address the limitations of RMSD, researchers have developed multiple complementary metrics that capture different aspects of structural similarity.

Distance-Dependent Measures

Global Distance Test (GDT) is a superposition-independent metric that measures the percentage of residues under a specified distance cutoff. The most common variant, GDT_TS, averages the percentages of Cα atoms falling under cutoffs of 1, 2, 4, and 8Å after optimal superposition [63]. This approach reduces sensitivity to outliers by focusing on the largest superimposable core.

Template Modeling Score (TM-score) normalizes the agreement between structures based on protein length, providing a more consistent measure across different protein sizes. TM-score ranges from 0 to 1, with values above 0.5 typically indicating the same fold, and values above 0.17 indicating random similarity [63]. The length normalization makes TM-score particularly valuable for comparing structures of different sizes.

Contact-Based Measures

Contact-based measures evaluate structural similarity by comparing residue-residue contact patterns rather than spatial positions. A contact is typically defined when two Cα atoms (or Cβ atoms) are within a specific distance cutoff (commonly 8Å) [3]. These measures are superposition-independent and more robust to structural variations that maintain the overall contact topology.

Contact Overlap calculates the percentage of common contacts between two structures, effectively capturing preserved interaction networks regardless of rigid-body movements [3].

Probabilistic and Weighted Measures

Recent approaches have incorporated probabilistic frameworks to account for heterogeneous structural precision. These methods model non-rigid displacements using heavy-tailed distributions that accommodate regions with large conformational differences while identifying a structurally invariant core [51].

Weighted RMSD (wRMSD) assigns continuous weights to individual atoms based on their probability of belonging to a conserved structural core. Unlike traditional RMSD, wRMSD iteratively updates weights to identify the maximally large structural core, making it particularly suitable for comparing structures with substantial conformational changes [51].

Table 2: Complementary Metrics for Protein Structure Assessment

Metric	Calculation Principle	Advantages	Typical Interpretation
RMSD	Root mean square of atomic distances after superposition	Intuitive; widely used	Lower values better (0 = identical); no inherent scale
GDT_TS	Average percentage of Cα atoms within multiple distance cutoffs (1, 2, 4, 8Å)	Less sensitive to outliers; emphasizes structural core	Higher values better (100 = identical); >50% generally good
TM-score	Length-normalized measure based on distance-dependent scale	Consistent across protein sizes; better fold-level discrimination	0-1 scale; >0.5 same fold; <0.17 random similarity
Contact Overlap	Percentage of common residue-residue contacts	Superposition-independent; captures interaction preservation	Higher values better (100% = identical contacts)
wRMSD	RMSD with iteratively determined weights for each atom	Identifies structural core; handles conformational changes	Lower values better; emphasizes conserved regions

Experimental Protocols for Comprehensive Structural Assessment

Protocol 1: Core Structural Alignment Using Iterative Weighted RMSD

Purpose: To identify the largest structurally conserved core between two protein structures, particularly when they exhibit significant conformational differences.

Materials:

• Two protein structures in PDB format
• Computational environment with Python/R and structural biology libraries
• Weighted RMSD implementation (e.g., using methodologies from [51])

Procedure:

• Initial Superposition: Perform standard RMSD minimization using all equivalent Cα atoms via Kabsch algorithm.
• Distance Calculation: Compute distances between all equivalent atom pairs after superposition.
• Weight Assignment: Assign weights to each atom pair using a probabilistic model (e.g., Gaussian scale mixture):
  • Model displacements using heavy-tailed distributions like Student's t-distribution
  • Estimate weights representing probability of belonging to structural core
• Iterative Refinement:
  • Recalculate superposition using weighted atom pairs
  • Update weights based on new displacement distances
  • Repeat until convergence of core identification
• Core Identification: Select atoms with weights above threshold (e.g., >0.5) as structural core
• Validation: Calculate both traditional RMSD and wRMSD on identified core

Expected Outcomes: The protocol identifies a structurally conserved core and provides a wRMSD value that more accurately reflects the similarity of this core, excluding divergent regions.

Protocol 2: Multi-Metric Structural Comparison

Purpose: To comprehensively evaluate structural similarity using complementary metrics that capture different aspects of structural conservation.

Materials:

• Two protein structures in PDB format
• Structural comparison software (e.g., TM-align, LGA, or PyMOL)
• Custom scripts for metric calculation and integration

Procedure:

• Global Superposition:
  • Superpose structures using standard RMSD minimization
  • Record global RMSD and visualization of alignment
• TM-score Calculation:
  • Calculate TM-score using length-normalized algorithm
  • Note specific regions contributing to score
• GDT Analysis:
  • Compute percentage of residues within 0.5, 1, 2, 4, and 8Ã… cutoffs
  • Plot cumulative distribution of distances
• Contact Map Comparison:
  • Generate residue-residue contact maps for both structures (8Ã… Cα cutoff)
  • Calculate contact overlap percentage
  • Identify conserved and divergent contact clusters
• Local Quality Assessment:
  • Calculate per-residue distance plot
  • Annotate functional regions (active sites, binding pockets)
  • Assess local preservation in critical functional areas
• Integrated Assessment:
  • Combine metrics into unified similarity assessment
  • Resolve discrepancies between different metrics

Expected Outcomes: A multi-faceted evaluation of structural similarity that highlights conserved core regions, preserved interaction networks, and local differences in functionally important areas.

Diagram 1: Multi-metric structural assessment workflow. The protocol integrates core-based, topological, and local metrics for comprehensive evaluation.

Table 3: Research Reagent Solutions for Structural Comparison

Resource	Type	Function	Example Tools/Implementations
Structural Alignment Algorithms	Software	Optimal superposition of structures	Kabsch algorithm, Quaternion-based alignment, LSQMAN
Multi-Metric Evaluation Packages	Software Suite	Comprehensive structural comparison	LGA, TM-align, PyMOL scripting, ChimeraX
Contact Map Generators	Computational Tool	Residue interaction network analysis	MDTraj, BioPython, VMD, CCP4
Probabilistic Modeling Frameworks	Statistical Library	Robust comparison of heterogeneous structures	Custom implementations based on [51] methodology
Benchmark Datasets	Reference Data	Method validation and calibration	ProteinBench [63], CASP/ CAPRI targets, SABMARK
Visualization Platforms	Software	Interactive structural analysis and rendering	PyMOL, ChimeraX, VMD, Jmol

While RMSD remains a valuable initial metric for protein structure comparison, its limitations necessitate a multi-metric approach for biologically meaningful assessment. The integration of core-identification methods (wRMSD), length-normalized scores (TM-score), contact-based measures, and local quality assessments provides a robust framework for structural analysis that aligns more closely with biological function and evolutionary relationships. As structural biology advances toward modeling larger complexes and conformational ensembles [64] [63], these complementary metrics will play an increasingly critical role in extracting meaningful insights from structural data, ultimately accelerating drug discovery and functional annotation of proteins.

In the field of structural biology, accurately quantifying the similarity between two protein three-dimensional structures is fundamental for understanding evolutionary relationships, assessing computational models, and classifying protein folds. The most traditionally used metric for this purpose is the Root Mean Square Deviation (RMSD), which calculates the average distance between equivalent atoms after optimal superposition of two structures [3] [17]. Despite its widespread use, RMSD possesses a significant drawback: its magnitude is inherently dependent on the length of the proteins being compared [65] [5]. This length dependence makes it difficult to interpret RMSD values across different protein sizes and to define universal similarity thresholds. Furthermore, RMSD is highly sensitive to local structural variations, such as divergent loops or terminal regions, which can dominate the score and obscure the overall global topological similarity [3].

To overcome these limitations, the Template Modeling Score (TM-score) was developed as a more robust and meaningful measure of global protein structural similarity [65]. The TM-score is designed to be sensitive to the global topology of the protein fold rather than local errors, and it incorporates a length-dependent normalization factor, resulting in a score that is largely independent of protein size [65] [66]. This article details the principles, calculation, and application of the TM-score, positioning it within the broader context of protein structure comparison research that traditionally relies on RMSD.

Theoretical Foundation of TM-score

The TM-score Equation

The TM-score is defined to assess the topological similarity between two protein structures. For a target structure and a template structure, the TM-score is calculated using the following equation [65]:

TM-score = max [ 1/(Ltarget) * Σ (i=1 to Lcommon) 1 / (1 + (di / d0(L_target))^2 ) ]

Where:

• L_target is the length of the target protein.
• L_common is the number of equivalent residue pairs.
• d_i is the distance between the i-th pair of equivalent Cα atoms after optimal superposition.
• d0(Ltarget) is a normalization factor defined as d0(Ltarget) = 1.24 * ∛(L_target - 15) - 1.8 [65].

The "max" indicates that the procedure identifies the optimal superposition matrix that maximizes the sum. The resulting TM-score ranges between 0 and 1, where a value of 1 indicates a perfect match between the two structures [65] [67].

Key Advantages Over RMSD

The design of the TM-score confers several critical advantages over the traditional RMSD:

• Sensitivity to Global Fold: The TM-score employs a weight function (1/(1 + (di/d0)^2)) that assigns higher weights to residue pairs with smaller distances and lower weights to pairs with larger distances [66]. This makes the score more sensitive to the global topology of the protein core than to local variations, which often involve flexible loops or termini [65] [66].
• Size Independence: The inclusion of the length-dependent scale d0(Ltarget) normalizes the distance errors. Consequently, the average TM-score for random, unrelated protein pairs is independent of protein size, typically around 0.3 with a standard deviation of 0.01, whereas the magnitude of RMSD for random pairs has a power-law dependence on protein length [65] [66].
• Intuitive Interpretation: The TM-score is bounded between 0 and 1, with statistically derived thresholds that have clear biological meanings regarding fold similarity, as detailed in Section 4.1.

Table 1: Fundamental Comparison Between TM-score and RMSD

Feature	TM-score	RMSD (Global)
Score Range	(0, 1]	(0, ∞)
Primary Sensitivity	Global topology	Local deviations
Length Dependence	Independent (Normalized)	Dependent
Average for Random Pairs	~0.3	Increases with protein size
Effect of Local Errors	Attenuated	Amplified

Computational Protocol for TM-score Calculation

The following diagram illustrates the standard workflow for calculating the TM-score between two protein structures, integrating both the basic calculation and the more advanced alignment procedure.

Detailed Methodological Steps

Input Structure Preparation

Begin by obtaining the three-dimensional coordinate files (typically in PDB or mmCIF format) for the two protein structures to be compared. The TM-score calculation is conventionally based on the Cα atoms of the protein backbone [65] [67]. Ensure the input files are correctly parsed, handling any alternate location indicators or residue insertions appropriately [67].

Determining Residue Correspondence

A critical step is defining which residues are equivalent in the two structures. Two primary approaches exist:

• Sequence-Dependent Mode: This mode assumes a strict one-to-one correspondence between residues based on their sequence order (e.g., when comparing a computational model to its known native structure with identical sequence). The TM-score program can be used for this purpose [67].
• Sequence-Independent Mode (Structural Alignment): When the residue correspondence is unknown or the sequences differ, a structural alignment algorithm must first be employed to identify equivalent residues. The TM-align algorithm is specifically designed for this task. It uses a heuristic approach combining gapless threading and dynamic programming to find the residue mapping that maximizes the TM-score [65] [68]. Other advanced algorithms like Fr-TM-align use a fragment-assembly approach to generate initial seed alignments, which are then refined, often resulting in improved TM-score and coverage compared to TM-align [68].

Optimal Superposition and Calculation

Once residue equivalences (L_common) are established, the algorithm performs an optimal rigid-body superposition of the two structures. This superposition is iteratively refined to maximize the value of the TM-score [65]. For each pair of equivalent Cα atoms, the distance d_i is measured after this optimal superposition. The normalization factor d_0 is computed based on the length of the target protein (L_target). Finally, all components are combined according to the TM-score equation.

Output and Interpretation

The procedure outputs the final TM-score, which quantifies the structural similarity. Additionally, most tools like TM-align and Fr-TM-align provide the residue alignment, the optimal rotation-translation matrix, and often a file for visualizing the superposed structures in molecular graphics software [67] [68].

Interpretation and Statistical Significance

Statistical Significance and Fold Classification

A major advantage of the TM-score is that its statistical significance has been rigorously calibrated against large databases of known protein structures, providing clear and quantitative interpretation guidelines [66].

• TM-score > 0.5: This strongly indicates that the two proteins share the same fold in the SCOP/CATH classification systems. The probability of two proteins having the same fold given a TM-score of 0.5 is very high. The P-value associated with a TM-score of 0.5 is approximately 5.5e-7, meaning one would need to consider over 1.8 million random protein pairs to find a score this high by chance [66] [67].
• TM-score < 0.17: Scores in this range correspond to the level of similarity expected from randomly chosen, unrelated proteins [67].
• Intermediate Scores (0.17-0.5): These indicate partial structural similarity, but not the same overall fold.

Table 2: Statistical Significance of TM-score Values

TM-score Range	Structural Relationship	Statistical Interpretation
> 0.5	Generally the same fold	High probability; P-value ~ 5.5 × 10⁻⁷
~0.3	Random correspondence	Average for unrelated pairs
< 0.17	Essentially no relationship	Similarity level of random proteins

TM-score in Practical Research Applications

TM-score has become an indispensable metric in various fields of structural biology and computational biophysics.

Assessment of Protein Structure Predictions

The TM-score is a standard metric in community-wide blind assessments of protein structure prediction (CASP), where it is used to evaluate the global correctness of submitted models against experimentally determined target structures [3] [66]. Its size independence allows for a fair comparison of models for proteins of different lengths.

Detection of Remote Homology and Fold Analysis

Because the TM-score is sensitive to global topology, it is highly effective for detecting remote evolutionary relationships that may not be apparent from sequence comparison alone [66]. It is also used in quantitative protein fold classification [66].

Application in Protein-Protein Complexes and Membrane Proteins

The utility of TM-score extends beyond single-chain proteins. It can be applied to assess the quality of predicted protein complex structures by treating the complex as a single entity [64] [67]. Furthermore, studies focusing on membrane proteins—which have distinct structural properties—have validated that fragment-based alignment methods like Fr-TM-align, which optimize the TM-score, are highly effective for this important class of proteins [69].

Table 3: Key Software Tools and Resources for TM-score Calculation

Tool/Resource Name	Type	Primary Function	Access/Download
TM-score	Standalone Program	Calculates TM-score based on given residue correspondence. Supports proteins, RNA, and DNA.	C++ and Fortran source code or executable available from the Zhang Lab [67].
TM-align	Standalone Program	Performs sequence-independent structural alignment to find the optimal TM-score.	Web server or source code from the Zhang Lab [65] [67].
Fr-TM-align	Standalone Program	An advanced algorithm using fragment assembly to generate improved initial alignments for higher TM-score.	Source code from http://cssb.biology.gatech.edu/skolnick/files/FrTMalign/ [68].
DeepSCFold	Advanced Pipeline	Uses deep learning to predict structural similarity from sequence; employs TM-score for benchmarking complex structures.	Method described in literature; demonstrates 11.6% TM-score improvement in CASP15 [64].

Advanced Considerations and Protocol Extensions

Comparison with Other Metrics (GDT_TS, RMSD)

While TM-score is a powerful global measure, it is often informative to use it alongside other metrics for a comprehensive assessment.

• GDTTS (Global Distance Test Total Score): This measure calculates the average percentage of Cα atoms that can be superposed under different distance cutoffs (e.g., 1, 2, 4, and 8 Ã…) [66]. Like RMSD, the average GDTTS score for random pairs is length-dependent [65]. TM-score provides a continuous and length-normalized alternative.
• RMSD: As discussed, RMSD remains useful for quantifying local, high-accuracy structural similarity, especially when comparing very similar conformations of the same protein.

Consensus Approaches for High-Confidence Alignment

For critical applications, such as aligning membrane proteins or structures with large conformational changes, relying on a single alignment method can be risky. Studies suggest that a consensus approach combining alignments from multiple high-performing methods (e.g., Fr-TM-align, DaliLite, MATT, FATCAT) can increase confidence. The agreement between different methods can be used to assign a reliability score to each position in the final alignment [69].

In protein structure comparison research, the Root Mean Square Deviation (RMSD) has traditionally been a widely used metric for quantifying structural similarity. However, RMSD suffers from significant limitations, particularly its sensitivity to outlier regions where small, incorrectly predicted segments can disproportionately inflate the overall score, thereby misrepresenting the quality of a largely accurate model [70] [71]. The Global Distance Test (GDT), also known as GDT_TS (Total Score), was developed to address these shortcomings by providing a more robust and biologically meaningful measure of structural similarity, especially in the context of protein structure prediction [70] [72].

GDT evaluates the quality of a predicted protein model against a reference structure by measuring the largest set of equivalent residues that can be superimposed within a defined distance cutoff. Unlike RMSD, which reports an average deviation, GDT produces a percentage score ranging from 0 to 100, where higher values indicate better model quality [70] [72]. This metric has become a cornerstone for evaluating predictions in the Critical Assessment of Structure Prediction (CASP) experiments, a community-wide benchmark for protein structure modeling techniques [70].

GDT Fundamentals and Comparison with RMSD

Core Principles and Mathematical Formulation

The GDT algorithm operates by identifying the largest subset of amino acid residues (specifically their Cα atoms) in a model structure that can be superimposed within a specified distance cutoff of their corresponding positions in an experimental reference structure after optimal rigid-body superposition [70]. The conventional GDT_TS score is calculated as the average of the percentages of residues superimposed under four distance thresholds: 1, 2, 4, and 8 Ångströms (Å) [70] [72]. This is formally expressed as:

GDTTS = (GDTP1 + GDTP2 + GDTP4 + GDT_P8) / 4

where GDT_Pn represents the percentage of residues under a distance cutoff of ≤ n Å [72].

For high-accuracy models, a more stringent variant called GDT_HA (High Accuracy) is computed using smaller cutoff distances: 0.5, 1, 2, and 4 Ã… [70] [72]. This metric more heavily penalizes larger deviations from the reference structure.

Comparative Analysis: GDT vs. RMSD

Table 1: Fundamental differences between GDT and RMSD

Feature	GDT (GDT_TS)	RMSD
Core Principle	Maximizes percentage of residues within distance cutoffs	Averages Euclidean distances of all atom pairs
Output Scale	0-100% (higher is better)	0-∞ Å (lower is better)
Sensitivity to Outliers	Robust	Highly sensitive
Interpretation	Intuitive percentage	Varies with protein size
Standard Cutoffs	1, 2, 4, 8 Ã…	Not applicable

The fundamental difference lies in their approach to structural deviation. RMSD calculates the square root of the average squared distance between corresponding atoms after superposition, making it highly susceptible to small, poorly predicted regions [71]. In contrast, GDT focuses on the maximal consensus between structures, effectively identifying the core correctly modeled regions while mitigating the influence of outliers [70] [71]. This makes GDT particularly valuable for evaluating protein models where accurate prediction of the structural core is more critical than peripheral loops or termini.

Computational Protocols and Methodologies

Algorithmic Workflow for GDT Calculation

The computation of GDT scores typically involves an iterative superposition process designed to find the optimal alignment that maximizes the number of residue pairs within the given distance thresholds [73]. The following diagram illustrates this workflow:

The algorithm begins by selecting starting points for alignment using a sliding window across the protein sequence [73]. For each window position, it enters an iterative loop where it:

• Performs a minimal-RMSD superposition on the current subset of residue pairs.
• Applies the resulting transformation to all residues in the model structure.
• Calculates the distances between all transformed model residues and their reference counterparts.
• Defines a new subset comprising only those residue pairs within the specified distance threshold.
• Repeats steps 1-4 until the subset converges (stops changing) [73].

This process is repeated for multiple starting points, and the largest subset of superposed residues ever observed is used to calculate the final GDT percentage for that threshold [73].

Practical Calculation Using the LGA Server

For researchers requiring standardized GDT assessments comparable to CASP results, the AS2TS/LGA server provides a reliable method. The following protocol outlines a two-run procedure to calculate GDT_TS:

Table 2: Two-run LGA server protocol for GDT_TS calculation

Step	Run 1: Optimal Superposition	Run 2: GDT_TS Calculation
1. Server	Access LGA at linum.proteinmodel.org	Same as Run 1
2. Input	Specify query (model) and reference structures	Paste full Run 1 output into Box 4
3. Parameters	-4 -o2 -gdc -lga_m -stral -d:4.0	-3 -o2 -gdc -lga_m -stral -d:4.0 -al
4. Execution	Submit job and complete Run 1	Submit job with cleared molecule fields
5. Output	Contains optimal superposition	Contains raw GDT_TS value
6. Adjustment	Not applicable	Adjust for full reference length: Final GDTTS = RawScore × (AlignedResidues / TotalReference_Residues) [74]

This method ensures the superposition is optimized before the final GDT calculation, aligning with practices used in CASP evaluation [74]. The adjustment in Step 6 is crucial when the aligned region represents only a portion of the full reference structure.

Advanced Variations and Extensions

The core GDT_TS metric has been extended to address specific assessment needs and to leverage more detailed structural information:

• GDT_HA (High Accuracy): Uses stricter distance cutoffs (0.5, 1, 2, and 4 Ã…) to evaluate models where high precision is expected, penalizing larger deviations more severely [70] [72].
• GDC (Global Distance Calculation): Extends the GDT concept beyond Cα atoms. GDCsc uses a predefined "characteristic atom" near the end of each side chain, while GDCall performs an all-atom comparison, providing a more comprehensive assessment of model quality [70].
• Algorithmic Optimizations: Traditional GDT calculations use heuristics. Advanced tools like OptGDT provide algorithms with theoretical guarantees, finding nearly optimal GDT scores and potentially improving matched residue counts by 10% or more for some models [71].

Table 3: Key computational tools and resources for GDT analysis

Resource Name	Type/Function	Key Application
LGA (Local-Global Alignment)	Structure Alignment Program	Original GDT implementation; CASP standard [70]
AS2TS/LGA Server	Web Service	Online GDT calculation with CASP-comparable parameters [74]
OpenStructure GDT Module	Programming Library	Integrable GDT function for custom analysis pipelines [73]
OptGDT	Algorithmic Tool	Computes theoretically guaranteed accurate GDT scores [71]
PDB (Protein Data Bank)	Reference Database	Source of experimentally-determined reference structures [75]

The Global Distance Test represents a significant advancement over RMSD for assessing protein structural models. Its robustness to local errors, intuitive percentage-based scale, and flexibility through various extensions (GDT_HA, GDC) make it an indispensable metric in structural bioinformatics. As the field progresses with advances in deep learning and generative models for protein structure [76] [75], GDT continues to provide a reliable standard for quantifying model accuracy, driving improvements in prediction methodologies, and ultimately enhancing our understanding of protein structure and function.

Quantifying the differences between protein three-dimensional structures is a fundamental task in structural biology, with critical applications in protein classification, evolutionary studies, and drug discovery [3]. While Root Mean Square Deviation (RMSD) has been the traditional measure for structural comparison, it possesses significant limitations that have driven the development of alternative approaches [3]. Contact-based measures represent a powerful superposition-independent methodology that overcomes many RMSD shortcomings by focusing on the patterns of atomic interactions within protein structures rather than the spatial positions of atoms after rigid-body alignment [3] [77].

The core limitation of RMSD lies in its sensitivity to outlier regions—the measure is dominated by the largest error between compared structures [3]. This means that two structures that are essentially identical except for the position of a single flexible loop or terminus will display a high global RMSD, potentially masking their overall structural similarity. Furthermore, RMSD values are highly dependent on the quality of the structural superposition, which itself is an ambiguous task with multiple potential solutions optimizing different parameters [3]. Contact-based methods circumvent these issues by eliminating the need for structural superposition altogether, instead focusing on the conservation of residue-residue contacts, which are more directly related to structural and functional conservation [3] [77] [78].

Table 1: Core Limitations of RMSD and Advantages of Contact-Based Measures

Aspect	RMSD-Based Measures	Contact-Based Measures
Sensitivity to Outliers	Highly sensitive; dominated by largest deviations [3]	Robust; local deviations have limited impact on global score
Superposition Requirement	Mandatory; introduces ambiguity [3]	Not required; inherently superposition-independent [3]
Handling of Flexibility	Poor; global measure affected by flexible regions [3]	Good; can identify conserved core despite flexibility
Biological Relevance	Geometric similarity [3]	Directly related to interaction patterns and stability [78]
Computational Complexity	Generally fast once superposition is determined	Varies by method; can be computationally intensive [77]

Key Methodologies and Algorithms

Contact Map Overlap (CMO)

The Contact Map Overlap (CMO) method represents protein structures as symmetrical, square Boolean matrices where entries indicate whether two residues are in contact [77]. A contact is typically defined based on a distance threshold between specific atoms (often Cα or Cβ atoms). The structural alignment problem is then reformulated as finding the alignment that maximizes the overlap between the contact maps of two proteins [77]. Although this problem has been proven to be NP-hard, several effective computational approaches have been developed [77].

The GANGSTA (Genetic Algorithm for Non-sequential, Gapped protein STructure Alignment) algorithm implements a hierarchical approach to optimize CMO [77]. It first performs structure alignment at the secondary structure element (SSE) level using a genetic algorithm to maximize pair contacts and relative orientations between α-helices and β-strands. Subsequently, residue pair contacts from the best SSE alignments are optimized [77]. This method is particularly valuable because it can identify structural similarities independent of SSE connectivity, recognizing homologous folds even when the sequential order of secondary structure elements differs [77].

Figure 1: Contact Map Overlap Calculation Workflow

Residue Interaction Networks (RINs)

Residue Interaction Networks (RINs) provide a graph-based framework for analyzing protein structures, where residues are represented as nodes and their interactions as edges [78]. This approach simplifies and rationalizes structural information while preserving the most relevant features of the protein fold [78]. RINs can be constructed using various interaction criteria, including side-chain contacts, hydrogen bonding, and spatial proximity. The resulting networks can then be analyzed using graph theory metrics to quantify structural similarity, identify key stabilizing residues, and detect functional sites [78].

The rise of accurate protein structure prediction tools like AlphaFold has significantly increased the importance of RINs, as they provide a powerful framework for analyzing and interpreting the surge in available structural data [78]. RINs can be effectively combined with other structural biology methods, including molecular dynamics simulations and artificial intelligence frameworks, to study protein behavior across different timescales—from conformational changes to long-term evolutionary divergence [78].

Contact Accepted Mutation (CAO) Model

The Contact Accepted Mutation (CAO) model represents a hybrid approach that unifies sequence and structural information into a single scoring matrix [79]. Unlike traditional substitution matrices like PAM (Point Accepted Mutation) that only consider residue replacements, CAO models the evolutionary interchange of structurally defined side-chain contacts [79]. This approach introduces critical structural information into protein sequence alignments, enabling detection of similarities between structurally conserved sequences even without apparent sequence similarity [79].

The CAO method evaluates the compatibility of residue changes at both positions in a pairwise interaction, making it closer in spirit to a substitution matrix that accounts for structural interactions [79]. Benchmarking on standard databases like homstrad and CATH has demonstrated that CAO scores coherently reflect the structural quality of sequence alignments, with particular value for homology modeling and threading techniques [79].

Experimental Protocols and Implementation

Protocol: Calculating Contact Map Overlap Using GANGSTA

Objective: Perform pairwise protein structure alignment using the GANGSTA algorithm to maximize Contact Map Overlap, independent of secondary structure element connectivity.

Table 2: Research Reagent Solutions for Contact-Based Analysis

Reagent/Resource	Function/Application	Specifications
GANGSTA Software	Performs connectivity-independent protein structure alignment using genetic algorithm [77]	Available through web server [77]
CATH Database	Provides curated protein domain classification for training and benchmarking [46]	Organized by Class, Architecture, Topology, Homologous Superfamily [46]
SCOP Database	Structural classification of proteins used for validation [77]	Family-level homologs provide reference alignments [77]
PDB Structures	Source of experimental protein structures for analysis [77]	Files contain 3D coordinate data for residues and atoms
Contact Map Generator	Converts 3D structural coordinates to residue contact maps [77]	Typically uses distance threshold (e.g., 8-12Å between Cα atoms)

Procedure:

• Input Preparation:

  • Obtain protein structures in PDB format from Protein Data Bank or predicted structures from AlphaFold Database.
  • Preprocess structures to identify and annotate secondary structure elements (SSEs) using DSSP or similar tools.

• SSE-Level Alignment:

  • Represent each protein as a graph where nodes are SSEs and edges represent spatial relationships.
  • Apply genetic algorithm to maximize pair contacts and relative orientations between SSEs.
  • Use gap penalty parameters to control for omitted SSEs in alignment.
  • Generate multiple candidate alignments through evolutionary algorithm operations.

• Residue-Level Refinement:

  • For best SSE alignments, optimize residue pair contacts using contact map overlap maximization.
  • Define residue contacts based on distance threshold (typically 8-12Ã… between Cα atoms).
  • Calculate CMO score representing the quality of structural alignment.

• Statistical Validation:

  • Compute P-value estimating the probability that a better score could occur by chance with unrelated proteins.
  • Consider alignments with P-value < 0.05 as statistically significant [77].
  • Validate against known structural classifications in SCOP or CATH databases.

Figure 2: GANGSTA Hierarchical Alignment Protocol

Protocol: Constructing and Analyzing Residue Interaction Networks

Objective: Create Residue Interaction Networks from protein structures and analyze them using graph theory metrics to quantify structural similarity.

Procedure:

• Network Construction:

  • Extract atomic coordinates from PDB files or predicted structures.
  • Define residue nodes based on amino acid positions in the structure.
  • Establish edges between residues using interaction criteria:
    • Spatial proximity (distance between Cα or Cβ atoms < 6.5-8Ã…)
    • Side-chain contacts (atoms within van der Waals radii)
    • Hydrogen bonding patterns
    • Hydrophobic interactions

• Graph Theory Analysis:

  • Calculate node centrality measures (degree, betweenness, closeness) to identify key residues.
  • Compute community structure to detect clusters of strongly interacting residues.
  • Determine network parameters (density, clustering coefficient, path lengths).

• Structural Comparison:

  • Compare RINs of different proteins using graph isomorphism measures.
  • Calculate similarity scores based on conserved interaction patterns.
  • Identify functionally important residues through conserved network motifs.

• Integration with Complementary Methods:

  • Combine with molecular dynamics simulations to study network evolution over time.
  • Integrate with artificial intelligence frameworks for pattern recognition in large datasets.
  • Correlate with evolutionary conservation data to identify structurally constrained regions.

Applications and Case Studies

Contact-based measures have demonstrated significant utility across diverse applications in structural biology and bioinformatics. The table below highlights key application areas with specific examples and benefits of contact-based approaches.

Table 3: Applications of Contact-Based Structure Comparison

Application Area	Specific Use Case	Advantage over RMSD
Detection of Non-sequential Similarity	Identifying Rossmann fold variants with different SSE connectivity [77]	Recognizes architectural similarity despite different polypeptide chain connectivity [77]
Homology Modeling	CAO model for improving sequence-structure alignment quality [79]	Unifies sequence and structure information; better detection of distant homologs [79]
Thermostability Analysis	Using RINs to identify key interaction networks in thermophilic proteins [78]	Reveals stabilizing residue clusters rather than global geometric similarity
Allosteric Mechanism Studies	Analyzing communication pathways in proteins using RIN centrality [78]	Captures interaction pathways irrelevant to spatial proximity alone
Evolutionary Studies	Tracking structural conservation despite sequence divergence [78]	Focuses on functionally critical interaction patterns

A compelling case study demonstrating the power of contact-based methods involves the structural alignment of SCOP domains 2uagA1 and 1gkuB1, which share an incomplete Rossmann structure motif but have different SSE connectivities [77]. While these proteins belong to different fold and superfamily categories in SCOP and would be challenging to align using traditional sequential methods, GANGSTA successfully aligned them with a statistically significant P-value (< 0.05) without introducing SSE gaps [77]. This example illustrates how contact-based approaches can reveal meaningful structural relationships that might be missed by sequence-order-dependent methods.

The CAO model has been benchmarked on standard databases including homstrad and CATH, demonstrating its ability to yield scores that coherently reflect structural alignment quality [79]. In comparisons with traditional PAM matrices and RMSD measures, CAO effectively bridges the gap between purely sequence-based and purely structure-based approaches, offering a unified framework that captures both evolutionary and structural constraints [79].

The revolutionary progress in protein structure prediction, led by deep learning tools like AlphaFold2, has generated hundreds of millions of protein models [50]. This explosion of structural data has created an urgent need for robust and efficient methods to compare, validate, and interpret these models. While the Root Mean Square Deviation (RMSD) remains a fundamental metric in structural biology, relying on it exclusively can lead to incomplete or misleading conclusions, especially for proteins with complex domain arrangements or flexible regions.

Selecting an appropriate metric requires understanding that each quantification method illuminates different aspects of structural similarity. This framework provides researchers with a systematic approach to metric selection based on their specific biological question, the characteristics of the proteins being compared, and the scale of their analysis. Proper metric selection is particularly crucial when working with challenging targets such as snake venom toxins or short antimicrobial peptides, where proteins may contain flexible loops or intrinsic disorder that complicate traditional analysis [80] [81].

Key Metrics and Their Underlying Principles

Traditional and Global Metrics

Root Mean Square Deviation (RMSD) calculates the average distance between superimposed atoms after optimal alignment, providing a direct measure of atomic-level differences. However, its sensitivity to outlier regions and requirement for pre-alignment can make it suboptimal for detecting remote homology. Template Modeling Score (TM-score) improves upon RMSD by using a length-dependent scale to weight local distances, making it more sensitive to global fold similarity than precise atomic positions [82]. Global Distance Test (GDDT) and Local Distance Difference Test (LDDT) assess the reliability of local atomic interactions by comparing distance differences within a structure, with LDDT being particularly valuable for evaluating model quality without a reference structure [82].

Local and Alignment-Free Metrics

For analyzing specific functional regions, local alignment scores focus on structurally similar subsets between proteins, which is valuable for identifying conserved active sites. 3Di similarity scores, implemented in Foldseek, describe tertiary amino acid interactions as sequences over a structural alphabet, enabling rapid detection of structural homology independent of sequence similarity [82]. Weighted Contact Number (WCN) captures local structural environments by quantifying the spatial density around each residue, providing insights into structural compactness [16].

Table 1: Key Protein Structure Comparison Metrics and Their Applications

Metric	Principle	Strength	Limitation	Ideal Use Case
RMSD	Average distance between equivalent atoms after superposition	Intuitive physical interpretation; Sensitive to small conformational changes	Highly sensitive to outlier regions; Requires predefined residue correspondence	Comparing very similar structures; Analyzing molecular dynamics trajectories
TM-score	Length-scaled measure of global fold similarity	Robust to local structural variations; Better for detecting remote homology	Less sensitive to local precision; Requires structural alignment	Determining overall fold similarity; Classifying protein structural relationships
LDDT	Local distance difference comparison without superposition	Reference-free evaluation; Captures local geometry quality	Does not require global superposition; May miss global arrangement issues	Model quality assessment; Validating predicted structures
3Di Score	Tertiary interaction patterns encoded as structural strings	Extremely fast comparison; Sensitive to structural conservation	Limited atomic detail; Dependent on alphabet quality	Large-scale database searches; Remote homology detection

Decision Framework for Metric Selection

The following workflow provides a systematic approach for selecting the most appropriate protein structure comparison metric based on research goals, system characteristics, and practical constraints.

Decision Workflow for Metric Selection

Define the Primary Research Objective

The first step involves precisely defining your research question, as different objectives demand different metrics:

• Global Fold Similarity: When determining whether two proteins share the same overall architecture, TM-score is preferable to RMSD because it is less sensitive to local variations and provides better discrimination between similar and dissimilar folds [82]. For example, when comparing predicted structures of snake venom toxins to known structures, TM-score would reliably identify shared folds despite variations in flexible loop regions [80].

• Local Feature Analysis: For investigating specific functional regions like active sites or binding pockets, combine local alignment approaches with 3Di similarity scores. These methods can identify local structural conservation even when global folds differ, which is particularly valuable for studying evolutionary relationships in multi-domain proteins [82].

• Large-Scale Database Searches: When scanning massive databases like the AlphaFold Database (over 214 million structures) or ESM Atlas (over 617 million structures), efficiency becomes critical [82] [50]. Foldseek and SARST2 use structural alphabets to achieve speeds four to five orders of magnitude faster than traditional structural aligners while maintaining high sensitivity [16] [82].

• Model Quality Assessment: For evaluating predicted structures or experimental models, LDDT provides a reference-free assessment of local geometry, while clash scores and Ramachandran analysis validate stereochemical合理性 [83] [81].

Consider Structure Characteristics

The nature of the structures being compared significantly impacts metric performance:

• Flexible or Multi-domain Proteins: For proteins with flexible regions or multiple domains, TM-score and Foldseek outperform RMSD because they are less sensitive to domain rearrangements and flexible regions [82]. Foldseek particularly excels at detecting homologous structured segments even when their relative orientations differ [82].

• Rigid, Single-Domain Structures: For well-structured, single-domain proteins where precise atomic positioning is important, RMSD provides valuable quantitative information about structural differences, especially when combined with TM-score for context [81].

• Challenging Targets: Short peptides, toxins, and proteins with intrinsic disorder require special consideration. Research indicates that different modeling algorithms (AlphaFold, PEP-FOLD, Threading) produce varying results for these targets, suggesting the need for multi-method validation that combines multiple metrics [80] [81].

Account for Practical Constraints

• Computational Resources: For large-scale analyses, the tremendous speed advantage of tools like Foldseek (23,000x faster than TM-align) and SARST2 (faster than BLAST with less memory requirements) makes them the only practical choice [16] [82].

• Reference Structure Availability: When reference structures are unavailable, LDDT and 3Di similarity can assess model quality and structural relationships without superposition [82].

Experimental Protocols for Metric Application

Protocol 1: Large-Scale Structural Database Search

This protocol enables efficient structural similarity searches against massive databases containing millions of structures.

Materials and Reagents:

• Query structure (PDB format or AlphaFold prediction)
• Target database (AlphaFold DB, ESM Atlas, or custom collection)
• Computational environment (ordinary personal computer sufficient for SARST2/Foldseek)

Procedure:

• Database Formatting: Convert the target database to a grouped format to reduce storage requirements. SARST2 can reduce AlphaFold DB storage from 59.7 TiB to only 0.5 TiB [16].
• Structural Encoding: Transform query and target structures using structural alphabets:
  • For Foldseek: Convert to 3Di strings representing tertiary interactions [82]
  • For SARST2: Generate linear encodings incorporating primary, secondary, and tertiary features [16]
• Filter-and-Refine Search:
  • Apply rapid k-mer based prefilters to discard clearly irrelevant structures
  • Use machine learning-enhanced filters (decision trees/neural networks) for candidate selection [16]
  • Perform refined alignment on remaining candidates using synthesized dynamic programming
• Result Validation: Assess hits using confidence measures:
  • Foldseek: E-values calculated via neural network based on 3Di composition [82]
  • SARST2: P-values based on weighted contact number scoring [16]

Troubleshooting Tip: If encountering high-scoring false positives, check for structures with correctly aligned segments but incorrect relative orientations—a known limitation of 3D aligners that Foldseek explicitly handles well [82].

Protocol 2: Multi-Metric Model Quality Assessment

This protocol provides comprehensive validation of protein structural models using complementary metrics.

Materials and Reagents:

• Protein structural models (experimental or predicted)
• Validation software (Foldseek, VADAR, MolProbity)
• Reference structures (if available for benchmark comparisons)

Procedure:

• Global Quality Assessment:
  • Calculate TM-score against reference structures (if available)
  • Compute LDDT scores for reference-free local geometry evaluation [82]
  • For cryo-EM structures, apply AI-based quality assessment like DAQ for residue-level quality evaluation [84]
• Local Geometry Validation:
  • Perform Ramachandran analysis to assess backbone torsion angles
  • Calculate clash scores to identify steric overlaps
  • Analyze rotamer outliers for side chain placement issues [83] [81]
• Map-Model Agreement (for experimental structures):
  • For cryo-EM structures, compute FSC curves to assess resolution [83]
  • Calculate Q-scores for map-model fit evaluation [84]
• Comparative Assessment:
  • Rank models by composite scores
  • Identify consistent issues across multiple metrics
  • Generate quality reports for decision-making

Troubleshooting Tip: When working with low-resolution cryo-EM structures (>3Ã…), focus more on global fold metrics (TM-score) than atomic-level validation (RMSD), as side chain positions are less reliable at lower resolutions [84] [83].

Research Reagent Solutions

Table 2: Essential Tools for Protein Structure Comparison Analysis

Tool/Resource	Type	Primary Function	Application Context
Foldseek	Software Suite	Rapid structural alignment via 3Di alphabet	Large-scale database searches; Remote homology detection
SARST2	Standalone Program	Filter-and-refine structural alignment	Resource-efficient searches on ordinary computers
TM-align	Algorithm	Template modeling score calculation	Pairwise structure comparison; Global fold assessment
LDDT	Validation Metric	Local distance difference test	Model quality assessment without reference
DAO	AI Tool	Residue-level quality assessment	Cryo-EM model validation and refinement
AlphaFold DB	Database	214+ million predicted structures	Source of structural models for comparison
PDB	Database	Experimentally determined structures	Benchmarking; Reference-based validation

Advanced Applications and Case Studies

Challenging Targets: Snake Venom Toxins and Short Peptides

Research on snake venom toxins demonstrates the importance of metric selection for challenging targets. These proteins often contain flexible loops and regions of intrinsic disorder that complicate analysis. A comparative study found that while AlphaFold2 performed best overall for toxin structure prediction, all tools struggled with disordered regions, particularly loops and propeptide regions [80]. In such cases, combining global metrics (TM-score for overall fold) with local metrics (3Di similarity for conserved domains) provides the most comprehensive assessment.

For short antimicrobial peptides, research indicates that different modeling algorithms complement each other: AlphaFold and Threading work better for hydrophobic peptides, while PEP-FOLD and Homology Modeling excel with hydrophilic peptides [81]. This suggests that metric selection should be tailored to both the target's characteristics and the modeling approach used.

Cryo-EM Structure Validation

The rapid growth of cryo-EM has created new challenges for structure validation. AI-based quality assessment methods like DAQ (Deep Learning-based Absolute Quality Assessment) have been developed specifically for cryo-EM models. These tools learn local density features to assess residue-level quality and can even automatically fix local errors identified during assessment [84]. For cryo-EM structures, it's essential to consider both map-model agreement metrics (like Q-scores) and geometric quality indicators, as regions of locally low resolution are prone to modeling errors.

Large-Scale Comparative Studies

When conducting analyses across thousands of structures, follow the ten rules for structural bioinformatic analysis [83]:

• Define precise biological selection criteria
• Implement rigorous quality control based on resolution and experimental method
• Remove redundancy through appropriate clustering
• Use control datasets to benchmark performance
• Connect structures to external databases for functional annotation

These practices ensure that metric-based comparisons yield biologically meaningful insights rather than computational artifacts.

Selecting appropriate metrics for protein structure comparison requires careful consideration of research objectives, structural characteristics, and practical constraints. No single metric provides a complete picture of structural relationships. RMSD remains valuable for atomic-level comparisons of similar structures, while TM-score better captures global fold similarity, especially for flexible proteins. For large-scale database searches, 3Di-based methods like Foldseek and SARST2 offer unprecedented speed without sacrificing sensitivity. When evaluating model quality, LDDT provides reference-free assessment of local geometry.

The most robust structural analyses combine multiple complementary metrics tailored to the specific research question. As structural databases continue to expand exponentially, with resources like the AlphaFold Database now containing over 214 million predictions [50], the framework presented here will help researchers navigate the complex landscape of structural comparison metrics to extract biologically meaningful insights from this wealth of structural data.

Conclusion

RMSD remains an indispensable, though imperfect, tool for quantifying protein structural similarity. A thorough understanding of its calculation, inherent limitations—such as sensitivity to outliers and protein size—and the context provided by complementary metrics like TM-score and GDT is crucial for robust structural analysis. For researchers in drug development and biomedical science, mastering these concepts enables more accurate assessment of computational models, deeper insights into protein dynamics and conformational changes, and more reliable structure-based drug design. As the field advances with increasingly sophisticated AI-predicted models, the principles of careful structural comparison will only grow in importance for validating hypotheses and translating structural data into clinical breakthroughs.

References

• 1. Root mean square deviation [https://en.wikipedia.org/wiki/Root_mean_square_deviation]
• 2. calculate RMSD between two structures 2025 [https://toolsriver.com/calculate-rmsd-between-two-structures/]
• 3. Methods of protein structure comparison - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC4321859/]
• 4. Machine learning analysis of molecular dynamics ... [https://www.nature.com/articles/s41598-025-11392-1]
• 5. A normalized root-mean-spuare distance for comparing ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2374114/]
• 6. Comparing Structures [https://docs.rosettacommons.org/docs/latest/getting_started/Comparing-Structures]
• 7. Structural alignment software [https://en.wikipedia.org/wiki/Structural_alignment_software]
• 8. Structure alignment of ligands considering full flexibility ... [https://www.sciencedirect.com/science/article/pii/S2001037022005414]
• 9. I have several protein structures – what to do and where ... [https://310.ai/blog/several-protein-structures]
• 10. Pairwise Structure Alignment [https://www.rcsb.org/docs/tools/pairwise-structure-alignment]
• 11. root mean square (RMS) [https://byjus.com/maths/root-mean-square/]
• 12. Root Mean Square Error (RMSE) [https://statisticsbyjim.com/regression/root-mean-square-error-rmse/]
• 13. Lesson 11: RMSD Between Two Structures [https://charmm-gui.org/?doc=lecture&module=scientific&lesson=11]
• 14. Significance of Root-Mean-Square Deviation in Comparing ... [https://www.sciencedirect.com/science/article/abs/pii/S0022283684710175]
• 15. Difference observed in protein RMSD between different ... [https://gromacs.bioexcel.eu/t/difference-observed-in-protein-rmsd-between-different-complexes-but-protein-is-same/8444]
• 16. SARST2 high-throughput and resource-efficient protein ... [https://www.nature.com/articles/s41467-025-63757-9]
• 17. Root mean square deviation of atomic positions [https://en.wikipedia.org/wiki/Root_mean_square_deviation_of_atomic_positions]
• 18. Protein Structure Comparison [http://openmopac.net/manual/Protein_structure_comparison.html]
• 19. Fast protein structure comparison through effective ... [https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1009986]
• 20. EnsembleFlex: Protein structure ensemble analysis made ... [https://www.sciencedirect.com/science/article/pii/S0969212625002497]
• 21. Lie-RMSD: A Gradient-Based Framework for Protein ... [https://arxiv.org/html/2508.17010v1]
• 22. Gaussian-Weighted RMSD Superposition of Proteins [https://www.sciencedirect.com/science/article/pii/S0006349506726315]
• 23. Fast protein structure comparison through effective ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8982879/]
• 24. Root mean square deviations in structure [https://manual.gromacs.org/current/reference-manual/analysis/rmsd.html]
• 25. SWISS-MODEL [https://swissmodel.expasy.org/]
• 26. The difficulty of protein structure alignment under the RMSD [https://pmc.ncbi.nlm.nih.gov/articles/PMC3599502/]
• 27. Protein Models Docking Benchmark 2 - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC4400263/]
• 28. Benchmarking AlphaFold2 on peptide structure prediction [https://www.sciencedirect.com/science/article/pii/S0969212622004798]
• 29. DockRMSD: an open-source tool for atom mapping and ... [https://jcheminf.biomedcentral.com/articles/10.1186/s13321-019-0362-7]
• 30. charnley/rmsd: Calculate Root-mean-square deviation ... [https://github.com/charnley/rmsd]
• 31. rmsd [https://pypi.org/project/rmsd/]
• 32. MaxCluster - A tool for Protein Structure Comparison and ... [https://www.sbg.bio.ic.ac.uk/maxcluster/]
• 33. Which software is suitable to calculate the root mean ... [https://chemistry.stackexchange.com/questions/15890/which-software-is-suitable-to-calculate-the-root-mean-square-deviation-between-t]
• 34. Queries about RMSD for Polymer? - GROMACS forums [https://gromacs.bioexcel.eu/t/queries-about-rmsd-for-polymer/4176]
• 35. AlphaFold Protein Structure Database [https://alphafold.ebi.ac.uk/]
• 36. Article A unified approach to sequential and non- ... [https://www.sciencedirect.com/science/article/pii/S2589004222014900]
• 37. Sequence alignment [https://en.wikipedia.org/wiki/Sequence_alignment]
• 38. Comparison of pairwise alignment methods [https://www.dnastar.com/manuals/MegAlignPro/17.3.1/en/topic/comparison-of-pairwise-alignment-methods]
• 39. Advancements in protein structure prediction [https://www.sciencedirect.com/science/article/abs/pii/S0010482525001921]
• 40. an open-source tool for atom mapping and RMSD calculation ... [https://pubmed.ncbi.nlm.nih.gov/31175455/]
• 41. spyrmsd: symmetry-corrected RMSD calculations in Python [https://jcheminf.biomedcentral.com/articles/10.1186/s13321-020-00455-2]
• 42. DockRMSD: Docking Pose Distance Calculation [https://aideepmed.com/DockRMSD/]
• 43. Measures of quality [https://bio-protocol.org/exchange/minidetail?id=614542&type=30]
• 44. Predicting the conformational flexibility of antibody and T ... [https://www.nature.com/articles/s42256-025-01131-6]
• 45. A comprehensive application of FiveFold for conformation ... [https://www.nature.com/articles/s41598-025-17022-0]
• 46. Rprot-Vec: a deep learning approach for fast protein structure ... [https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-025-06213-1]
• 47. Prediction of MD‐derived protein flexibility from sequence [https://pmc.ncbi.nlm.nih.gov/articles/PMC12267886/]
• 48. what is the threshold RMSD value for determining protein structure... [https://www.biostars.org/p/356274/]
• 49. What is the RMSD and how to compute it with GROMACS - Compchems [https://www.compchems.com/what-is-the-rmsd-and-how-to-compute-it-with-gromacs/]
• 50. Emerging frontiers in protein structure prediction following ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11999738/]
• 51. Robust probabilistic superposition and comparison of protein ... [https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-11-363]
• 52. Comparative Analysis of Protein Structure Alignments - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC1959231/]
• 53. A graphic and command line protocol for quick and ... [https://www.nature.com/articles/s41596-025-01189-x]
• 54. LoCoHD: a metric for comparing local environments of proteins [https://pmc.ncbi.nlm.nih.gov/articles/PMC11091161/]
• 55. A novel method to compare protein structures using local ... [https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-12-344]
• 56. Align two or more 3D structures to a given structure - NCBI [https://www.ncbi.nlm.nih.gov/guide/howto/align-2-struct]
• 57. What is Root Mean Square Deviation (RMSD) and Its Role in ... [https://www.letstalkacademy.com/root-mean-square-deviation-protein-structure-comparison/]
• 58. Alignment of protein structures in the presence of domain ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2535786/]
• 59. A Mathematical Framework for Protein Structure Comparison [https://pmc.ncbi.nlm.nih.gov/articles/PMC3033361/]
• 60. Performance and Its Limits in Rigid Body Protein- ... [https://www.sciencedirect.com/science/article/pii/S0969212620302094]
• 61. Ten rules for a structural bioinformatic analysis [https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1013094]
• 62. Protein structure alignment beyond spatial proximity [https://www.nature.com/articles/srep01448]
• 63. ProteinBench: A Holistic Evaluation of Protein Foundation Models [https://arxiv.org/html/2409.06744v2]
• 64. High-accuracy protein complex structure modeling based ... [https://www.nature.com/articles/s41467-025-65090-7]
• 65. Template modeling score [https://en.wikipedia.org/wiki/Template_modeling_score]
• 66. How significant is a protein structure similarity with TM- ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2913670/]
• 67. TM-score: Quantitative assessment of similarity between ... [https://aideepmed.com/TM-score/]
• 68. Fr-TM-align: a new protein structural alignment method based ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2628391/]
• 69. Structure Alignment of Membrane Proteins: Accuracy ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4545697/]
• 70. - Wikipedia Global distance test [https://en.wikipedia.org/wiki/Global_distance_test]
• 71. Finding Nearly Optimal GDT Scores - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC3607910/]
• 72. | Foldit Wiki | Fandom GDT [https://foldit.fandom.com/wiki/GDT]
• 73. Global Distance Test - OpenStructure | GDT [https://openstructure.org/docs/2.11/mol/alg/gdt/]
• 74. Calculating GDT TS - Proteopedia, life in 3D [https://proteopedia.org/wiki/index.php/Calculating_GDT_TS]
• 75. Beyond static structures: protein dynamic conformations ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12262120/]
• 76. Assessing generative model coverage of protein structures ... [https://www.sciencedirect.com/science/article/abs/pii/S2405471225001802]
• 77. Connectivity independent protein-structure alignment [https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-7-510]
• 78. Decoding protein structures with residue interaction networks [https://www.sciencedirect.com/science/article/pii/S0968000425001951]
• 79. Testing homology with Contact Accepted mutatiOn (CAO) [https://www.sciencedirect.com/science/article/abs/pii/S1476927103000227]
• 80. A comparative study of protein structure prediction tools for ... [https://www.sciencedirect.com/science/article/pii/S0041010123003707]
• 81. A comparative study of computational modeling ... [https://www.nature.com/articles/s41598-025-16866-w]
• 82. Fast and accurate protein structure search with Foldseek [https://www.nature.com/articles/s41587-023-01773-0]
• 83. Ten rules for a structural bioinformatic analysis - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC12578330/]
• 84. AI-based quality assessment methods for protein structure ... [https://www.sciencedirect.com/science/article/pii/S2665928X25000017]